LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?
-
@李东岳 我用OpenFOAM-8也算了channel395,用tutorial算例计算,采用 @学流体的小明 提供的MATLAB程序中method2算的$U_\tau$:
- tutorial算例用的WALE模型,0文件夹其实不需设置
k和nuTilda,只需要设置p、U和nut。 - tutorial算例是给定了一个湍流初始场。一开始没注意删掉了,没有初始场到1000s计算不出湍流。初始湍流场的不同对结果是否影响会比较大?
- 一般认为开始计算的一段时间的湍流还没充分发展,计算平均场是都会剔除。tutorial算例提供的统计是从0时刻就开始统计。不过我尝试从1000s才开始统计,共计算5000s,结果与默认算例结果一致。
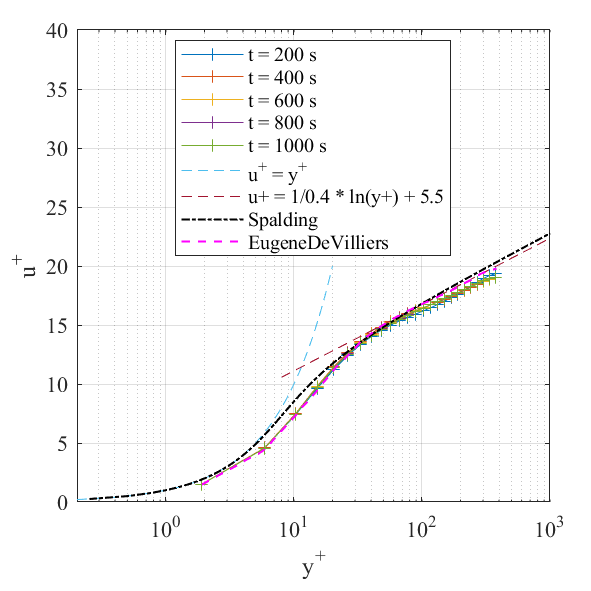
同时还提取了EugeneDeVilliers博士论文图5.5中6万网格的结果,其实跟我们的计算结果一致的,都是有偏差!推测他也是用method2算的。他的论文没有给出参考线,导致看起来结果很好。 图中Spalding曲线是根据《无痛苦NS方程笔记》中提到的公式画出对比。

(1)tutorial算例默认设置结果:从0秒开始统计

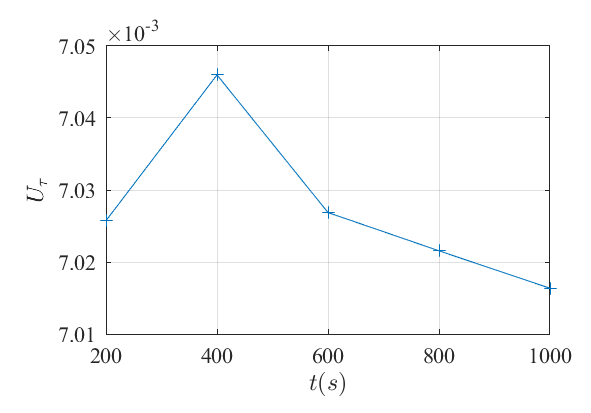
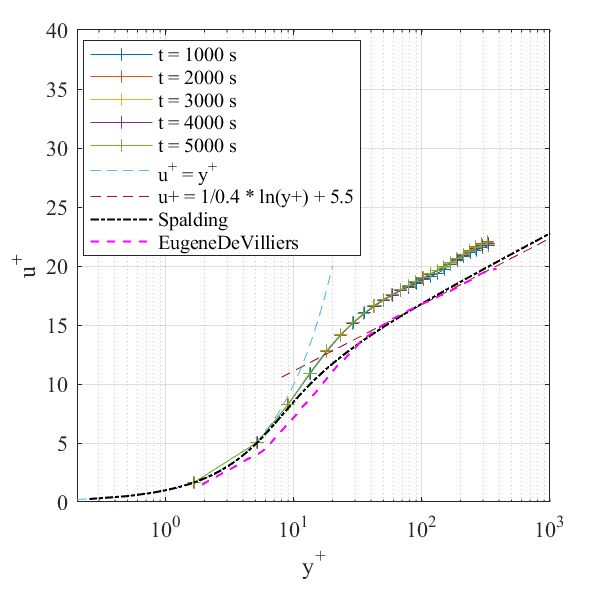
(2)从1000秒开始统计。1000s的结果其实是1000s这个时刻的瞬时结果,但对整个底面平均后,与后面时刻的结果基本一致。
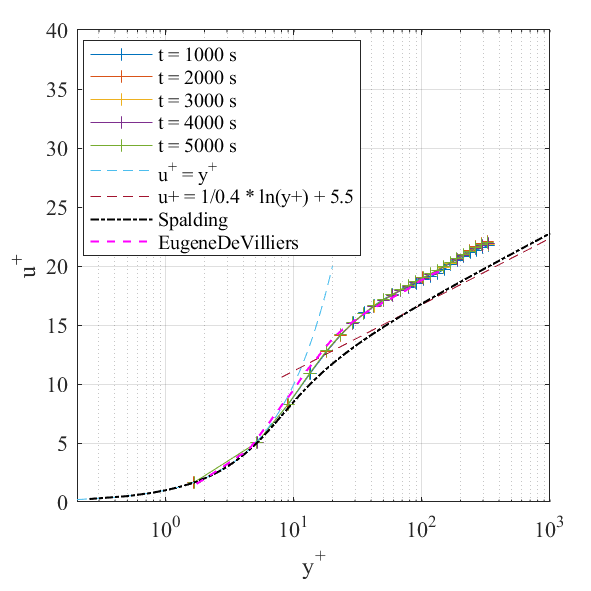
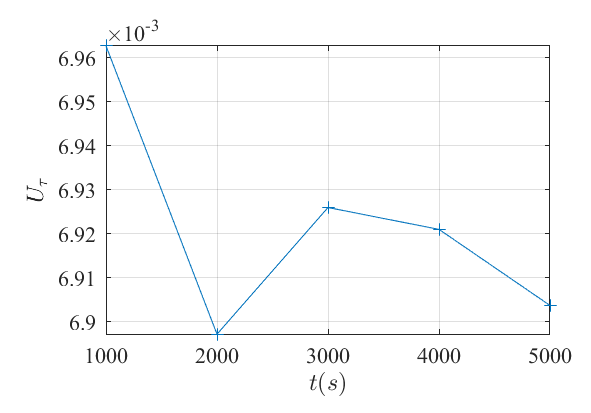
4. tutorial算例默认设置,method2计算结果都是在粘性子层结果较好,log区结果不吻合。尝试$U_\tau$按照method1取值,即$U_\tau=0.0079$,结果如下。说明了目前算例结果,改变$U_\tau$,只能满足粘性子层或者log区之一,是无法同时满足这两个区。想要同时满足,可能需要尝试加密网格之类方式
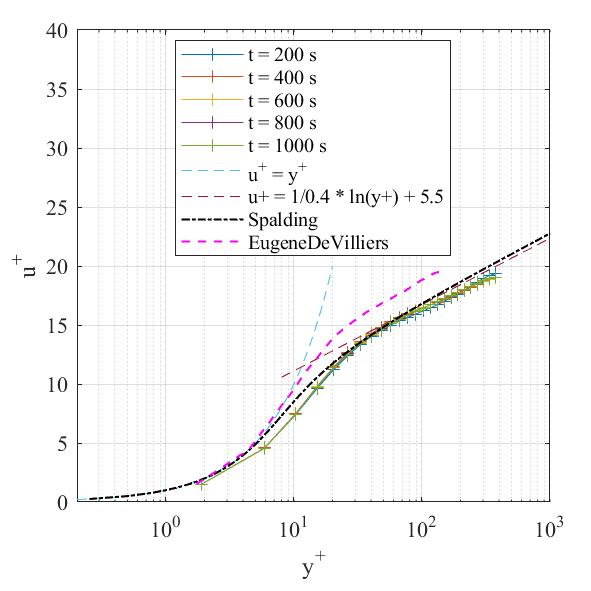
- tutorial算例用的WALE模型,0文件夹其实不需设置
-
http://dyfluid.com/boundaryFoam.html 我顺着这个里面的方程2,在y方向做积分,继续推了一下:
$$
\int\left(-\frac{\partial \tau_{xy}}{\partial y}\right)\rd y=-\int\left(\frac{\partial p}{ \partial x}\right)\rd y
$$$$
\tau_{xy}^h -\tau_{w}=-\tau_{w}=\frac{\partial p}{ \partial x}h
$$所以充分发展的管道,如果壁面剪切力知道的话,应该这样给一个压力梯度。
也不是不能大、不能小,设置得大了,槽道流速增加,会达到新的平衡的。
对,应该是。


 还得持续学习啊!
还得持续学习啊! -
 李 李东岳 被引用 于这个主题
李 李东岳 被引用 于这个主题
-
 学 学流体的小明 被引用 于这个主题
学 学流体的小明 被引用 于这个主题
-
并请教:槽道流LES计算的入口inflow速度场影响大吗?
我的计算域没有入口出口之分,沿流动方向的两个边界都是周期性的边界条件,展向也是周期性的边界条件。所以无法回答你的问题。
看起来你是采用了一种生成脉动速度的入口条件吗?
是的,用的就是EugeneDeVilliers在他博士论文中提到的初始化槽道流流场的方法。
-
谢谢。@学流体的小明
我的计算域没有入口出口之分,沿流动方向的两个边界都是周期性的边界条件,展向也是周期性的边界条件。所以无法回答你的问题。
我的算例也是周期边界的槽道流,其实应该是internalField初始场的影响。
前面我采用的是uniform的初始速度场,计算湍流雷诺数远达不到目标值。最近按你算例的codeStream代码加入了初始脉动速度,计算雷诺数比较接近目标值了。
以Re_tau=1000为例,我现在计算得到的雷诺数数值是910是的,用的就是EugeneDeVilliers在他博士论文中提到的初始化槽道流流场的方法。
EugeneDeVilliers大佬的论文提到了这种湍流需要加入初始扰动才能发展,这个初始化方法也有一个 perturbU的开源代码。不过codeStream的实现更方便

-
这个codeStream写的扰动,可以保证$\nabla\cdot\bfU=0$么
我只看到codeStream跟perturbU的代码是一致的,具体的公式在EugeneDeVilliers博士论文5.1.2章也能找到
-
-
@学流体的小明 大佬好,想问下当时你用方法三计算的时候,OpenFOAM中输出的
wallShearStress,有三个分量。$\tau_w$计算是如何计算的,是取了$\tau_x$,还是$\sqrt{\tau_x^2+\tau_y^2}$,还是$\sqrt{\tau_x^2+\tau_y^2+\tau_z^2}$?方法三:
通过paraview的filter - integrate variables - 查看 cellData,得到wallShearStress的和以及面积Area,计算固壁面上的wallShearStress平均值,再使用$$ {u_\tau } = \sqrt {\frac{{{\tau _w}}}{\rho }} $$
计算摩擦速度$ {u_\tau }$。注意不可压缩求解器中没有密度,则认为$\rho=1$。
结果是$u_{\tau } = 0.0066952$。