关于OpenFOAM中，多相流守恒性与鲁棒性的讨论

[四季之中的隐星]

首先，我们假设一个速度恒定，不考虑压力和体积力，但考虑相变的两相流动过程，此时，k相的控制方程有：


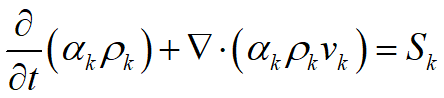
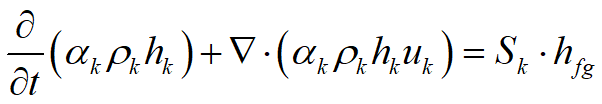
其中的Sk表示k相的源项。我们知道，对于一个小网格内，Sk如果较大，而从气到液体或者液体到气体的相变过程势必会在网格上引起额外的对流通量，因为相变会使得体积发生变化。
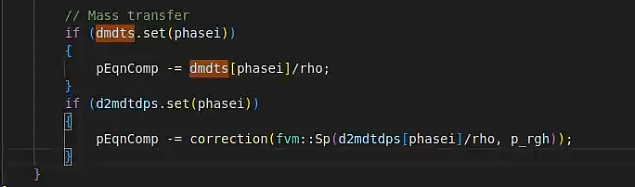
在OpenFOAM中所使用的欧拉多相流求解器multiphaseEulerFoam中，相分数方程并未做额外处理，但是在能量方程中，却多了一项，具体的有：
in file AnisothermalPhaseModel.C

···
    const tmp<volScalarField> tcontErr(this->continuityError());
    const volScalarField& contErr(tcontErr());
···
    tmp<fvScalarMatrix> tEEqn
    (
        fvm::ddt(alpha, rho, he)
      + fvm::div(alphaRhoPhi, he)
      - fvm::Sp(contErr, he)

      + fvc::ddt(alpha, rho, K) + fvc::div(alphaRhoPhi, K)
      - contErr*K

      + this->divq(he)
     ==
        alpha*this->Qdot()
    );

其中，continuityError()为
in file MovingPhaseModel.C

template<class BasePhaseModel>
void Foam::MovingPhaseModel<BasePhaseModel>::correctContinuityError
(
    const volScalarField& source
)
{
    volScalarField& rho = this->thermoRef().rho();

    continuityError_ = fvc::ddt(*this, rho) + fvc::div(alphaRhoPhi_) - source;
}

不难看出，当相变/源项存在时，为了防止体积溢出的部分的能量影响网格内能量的计算，添加了一个额外的连续性修正项contErr来消除溢出项的影响（实际上动量方程中也添加了该项）。但是，这样的方式显然会破坏全场内的能量与质量守恒，两相条件蒸发，网格内产生的膨胀体积应当输运到其他网格中，但是这样的处理方式显然没有对该过程进行考虑。
因为膨胀引起网格面额外通量的分析和计算过程本身十分复杂，考虑起来非常困难，因此只能牺牲一些守恒性换来鲁棒性。但是无论在openfoamwiki中的理论手册、李东岳老师还是其他商业软件中都没有把这一项写在理论说明的文档里。想请教一下各位老师和学者，这样的处理方式是两相求解领域的共识吗？

[李东岳]

其中的Sk表示k相的源项。我们知道，对于一个小网格内，Sk如果较大，而从气到液体或者液体到气体的相变过程势必会在网格上引起额外的对流通量，因为相变会使得体积发生变化。

这方面算法我没有看的太细。但是物理上是应该这个样子。openfoam这面怎么处理的？是某个网格k相体积分数到1之后，就进入到其他的网格单元了么。那周围网格单元的量是怎么分配的呢

[Tens]

@四季之中的隐星 不太了解multiphaseEulerFoam这个求解器，但是在compressibleInterFoam中，膨胀体积在相体积分数方程中好像是通过源项dgdt，然后MULES修正来处理的。
参考CompressibleInterFoam解析
我看phaseSystemSolve.C文件中好像也这样进行处理了

[四季之中的隐星]

@Tens dgdt是可压缩性项，而非源项项目，对应在李东岳老师的说明里是这个部分

[四季之中的隐星]

@李东岳 我目前感觉是在压力方程中进行了一下处理，但是我不太确定。这一项和原始动量方程，以及和连续性方程，能量方程的迭代修正方式。在压力方程中有个这个

这里面的dmdt就是实际上的源项，但是我目前还没看太明白，他怎么迭代回去到能量和连续性方程，以及这一项怎么和速度联系的。 最近还有一些其他的事情，这块代码啃的比较慢

[李东岳]

压力方程其实就是连续型方程。所以如果压力方程里面有源项，那说明连续性方程那面有了生成，可以理解。就是不知道他这个是怎么分配的。比如一个四边形2D的P网格单元，会有4个相邻单元。那这4个相邻单元的生成都是一样的么？看起来是通过dmdt来控制的。那我估计这个相邻单元的分配，dmdt在这4个网格单元应该不一样。并且应该是通量导致的dmdt变化。