气泡合并模型中的系数
-
最近在植入这个文章里边的改进的合并破碎模型发现系数有点不懂地地方；
用到的合并模型是PrinceBlanch模型
首先是这个碰撞区域计算
论文以及模型的老论文给的都是半径的和的平方。但是fluent以及openfoam官方api给的都是直径的和的平方：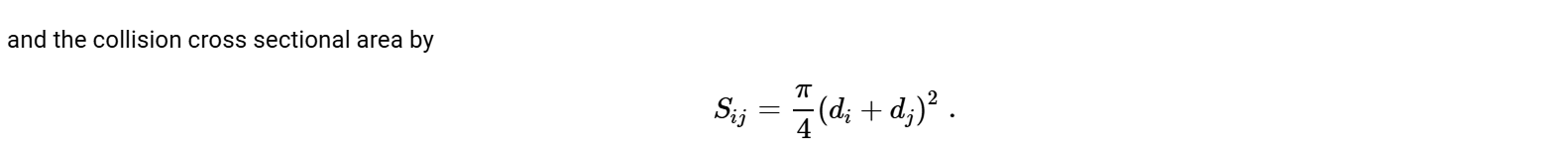
；
其次合并效率计算公式如下：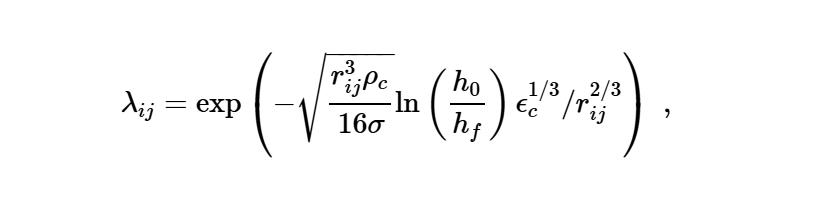
这篇论文给的如下：
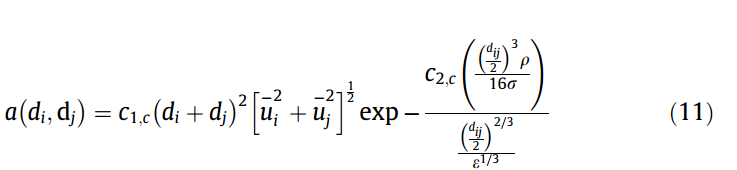他这个公式应该打错了少了个根号。那么他这里边的才也就是openfoam中的ln(h0/hf).openfoam的初始建议值是h0:1e-4,hf:1e-8.这样的话这个值应该是9.2.但是这个作者发的两篇ces在水中给的c2值为0.001 .差距很大 -
更新一下，看来这里边常数都是根据模拟结果凑着调整的
Another critical factor for the simulation of bubble column reactors is the closure model for coalescence and breakage. Various coalescence and breakage models have been examined in recent decades [39–44].Prince and Blanch [39] proposed a turbulent coalescence model of bubbles under the assumption of isotropic turbulence, which has been widely applied to bubble columns or stirrer vessels. In spite of its popularity, researchers concluded that the predicted coalescence rate in the Prince and Blanch model is overestimated for turbulence-induced coalescence [24,41–44]. Hence, to align the simulation results with experimental data, either coalescence or breakage rate is adjusted by multiplying with an arbitrary constant. However, there is still no general agreement in the literatures on the value of this multiplier and even contradictory conclusions were drawn. Chen et al increased the breakage rate by a factor of 10 and maintained the coalescence rate constant in their simulations [41]. Olmos et al [42] multiplied a constant of 0.075 for both the coalescence and breakage rates to fit the experimental data. As such, the justification of the coalescence or breakage model is weakened and the predictive capability of the numerical simulation is lost. Moreover, it is troublesome and time-consuming to tune the multiplier via the trial-and-error procedures. While the investigation of coalescence model will not be the focus of the present work, we improve the coalescence model with the slip velocity proposed by Bhole et al [44] and apply this model to the CFD-PBM simulations of a rectangular bubble column.气泡塔反应器模拟的另一个关键因素是聚结和破裂的闭合模型。近几十年来，人们研究了各种聚结和破裂模型 [39–44]。
Prince 和 Blanch [39] 在各向同性湍流假设下提出了一种气泡湍流聚结模型，该模型已广泛应用于气泡塔或搅拌器容器。尽管该模型很受欢迎，但研究人员得出结论，Prince 和 Blanch 模型中预测的湍流诱导聚结的聚结率被高估了 [24,41–44]。因此，为了使模拟结果与实验数据一致，聚结率或破裂率都通过乘以任意常数来调整。然而，文献中对这个乘数的值仍然没有普遍的共识，甚至得出了相互矛盾的结论。陈等人在他们的模拟中将破裂率提高了 10 倍，并保持聚结率恒定 [41]。 Olmos 等人 [42] 将聚结和破碎率乘以 0.075 的常数以拟合实验数据。这样一来，聚结或破碎模型的合理性就被削弱了，数值模拟的预测能力也丧失了。此外，通过反复试验的过程调整乘数既麻烦又耗时。虽然聚结模型的研究不是本研究的重点，但我们改进了 Bhole 等人 [44] 提出的滑移速度聚结模型，并将该模型应用于矩形气泡塔的 CFD-PBM 模拟。
