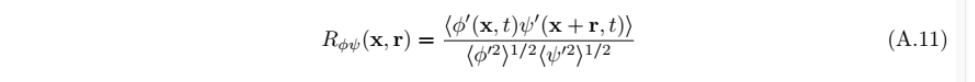周期性边界明渠的两点相关性分析Ruu、Rvv、Rww如何计算?
-
@liuxin 借这个楼再问一些相关的问题
相关性的定义,我看到两种。第一种是某个时刻的相关,第二种是在第一种的基础上,在时间上也进行了平均。
第一种定义见Pope, S. B. 2000 Turbulent Flows.

第二种定义我在这个报告中找到 https://www.researchgate.net/publication/304943166_Large-Eddy_Simulation_of_Turbulent_Channel_Flow 。可以看到时间 t 在平均之后消失,而且作者在前面也定义了此方括号包含了时间上的平均。

应该用哪一种互相关函数来证明计算域足够大呢?
Pope书中没有具体的DNS计算设置。
LES报告中的公式以及结果,看起来也都是第二种定义。
这两种定义的结果,画出来确实不太一样。我用$y^+=10$这个平面上的速度脉动来做互相关分析。
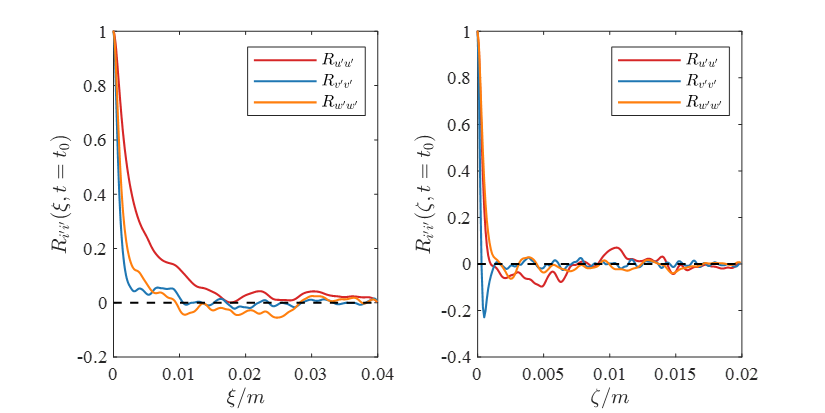
上图:某个时刻$t_0$的两点速度脉动的相关函数。可以看到它的起伏还是比较明显的,特别是在展向$z$方向,由于湍流的条带确实存在,随着间距$\zeta$的增大,相关函数是会在0的上下波动。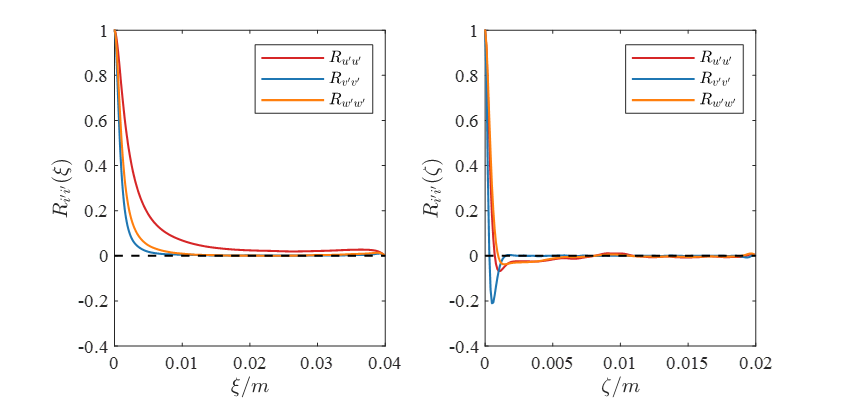
上图:某一段时间平均之后的两点速度脉动的相关函数。起伏消失,整个相关性曲线很平滑。
目前看起来,Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133-166.的结果是时间平均之后的两点相关,他们的标识里面也没带时间。
另外想问一下第一张图是那一片文章,有提到过是时间平均的还是某个时刻的吗?请大佬们指点🙏
-
- 这两个图分别对应 方法1 和 方法2 的计算结果吗,还是不同方向的结果?

- 对于方法1 ,这个写法是系综平均求相关函数,最后还要归一化得到相关系数。如果时间非平稳和空间非均匀,理论上统计量跟选择的参考点位置
x和时间t都相关。但槽道流的在展向和顺流向是均匀+时间平稳的,所以最后的统计特性都与参考位置参考点位置x和时间t都无关,所以可以用空间和时间一起平均得到最终统计量,of自带的postChannel工具就是这么做的。
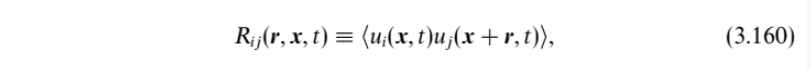
- 计算空间相关函数有2种方法:
(1)方法1,根据《Shin K, Hammond J. Fundamentals of signal processing for sound and vibration engineers[M]. England: John Wiley & Sons, 2008.》,已知在固定点位置,一条时间序列u(x=x0, y=y0, z=z0, t),针对这条时间序列求时间相关函数公式如下截图,在MATLAB中对应函数是xcorr。这种方法要求序列足够长,并且点数足够多,才能算的准确。

类似的,在某一固定时刻,沿着空间展向z的一条空间序列
u(x=x0, y=y0, z, t=t0),也一样可以用xcorr求空间相关函数,计算结果要准确,就要求这条序列的展向宽度要足够大,且点数足够多,否则计算结果就会偏差大。 如果计算域纵向足够长,把每条展向空间相关函数做空间平均,得到的结果应该也会比较准确。想要更准确就要加上每个时刻的平均,就要输出每个时刻的数据,计算量太大了,用空间平均了,其实时间平均应该就不用了,结果差别不会太大。(2)方法2,跟下面公式一样,计算两个序列的相关系数,对应MATLAB函数
corrcoef。已知展向上空间多个点A(x0, y0, zA, t)、B(x0, y0, zB, t)、C(x0, y0, zC, t)的时间序列,就可以假设选定A为参考点,依次计算出 AB、AC的相关系数,然后就可以把连成展向空间相关系数曲线。这种方法就要设置展向监测点,测量出每个点的时程数据,相对来说时程数据比空间数据(受限于计算域大小)更长,计算结果应该会比较准确。还可以设置多个不同x向位置的测点,再对计算的空间相关系数曲线平均,结果会更准确。 -
感谢大佬回复@coolhhh
这两个图分别对应 方法1 和 方法2 的计算结果吗,还是不同方向的结果?
不同方向的结果。$\xi$是$x$方向的间距,$\zeta$是$z$方向的间距。上面我画的都是相关系数,也就是相关函数进行了归一化,所以在间距$\xi$或$\zeta$为0时,相关系数都为1。
看起来对于槽道流这种展向和顺流向是均匀+时间平稳的流动是可以用时间平均之后的。问AI,AI也是这么说的。
我的数据在时间上和空间上也比较多,$\phi(x,z,y=y_0,t)$每个计算网格的值都输出了,时间上也以很小的时间间隔输出了一段时间。无论是时间上的相关系数还是空间上的,计算起来都没什么难度。