求助:液池热毛细对流算例,已编译好求解器和算例,但就是和文献自编程序不一样
-
在提问题之前,首先给大家科普一下热毛细对流
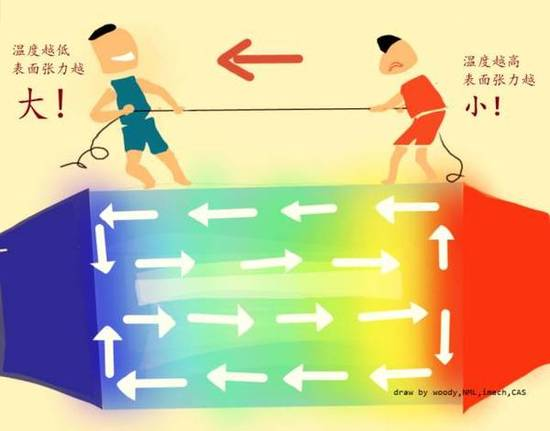
当液池两端的温度不一样的时候,一端热一端冷,在液体表面张力的作用下,会产生热毛细流动。热毛细流动是空间微重力环境下的主要自然对流形式。
表面张力会随着温度变化,温度高的地方表面张力低,温度低的地方表面张力高,表面张力不均匀成为驱动微重力流动的因素。由于表面张力又称毛细力,所以这种表面张力温度效应驱动流动,又称为热毛细流动,或者叫做Marangoni对流。
液池的形状是下面这样
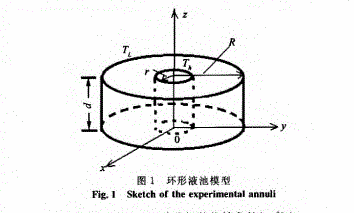
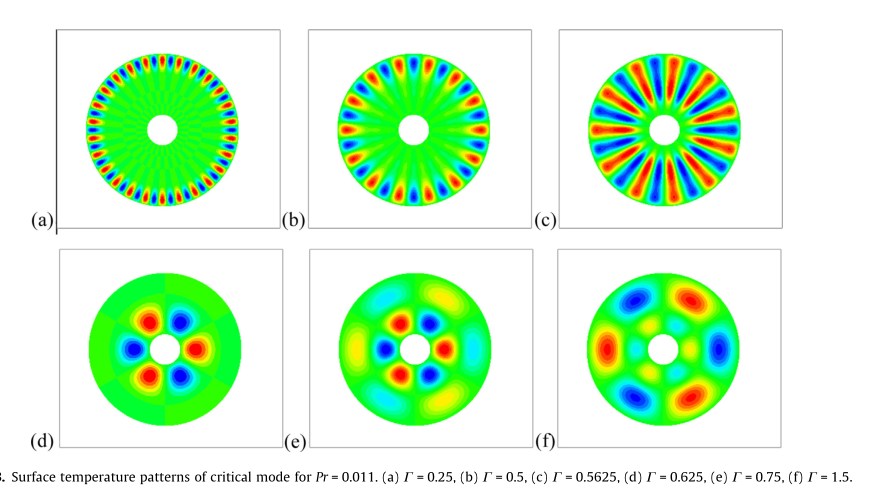
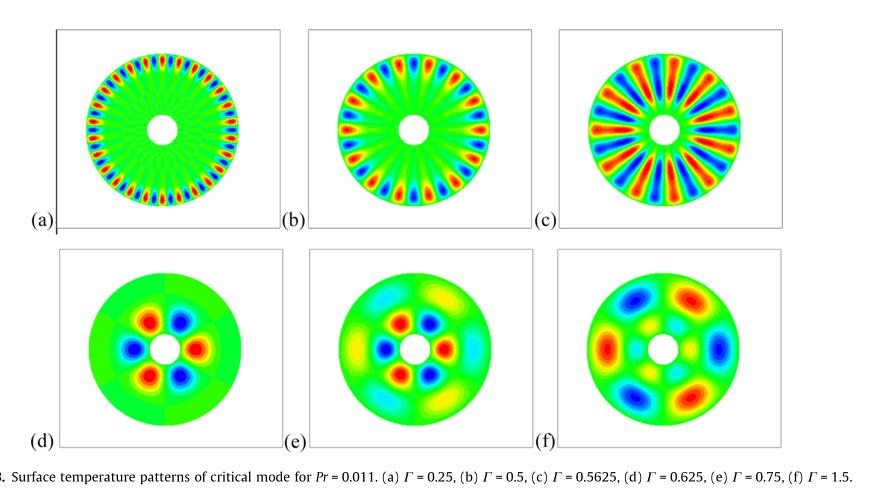
这个液池上表面是自由液面,其他是墙壁,内外环给不同的温度,使其在自由面造成热毛细对流的效果,我参考了这个文献
https://doi.org/10.1016/j.ijheatmasstransfer.2018.10.016
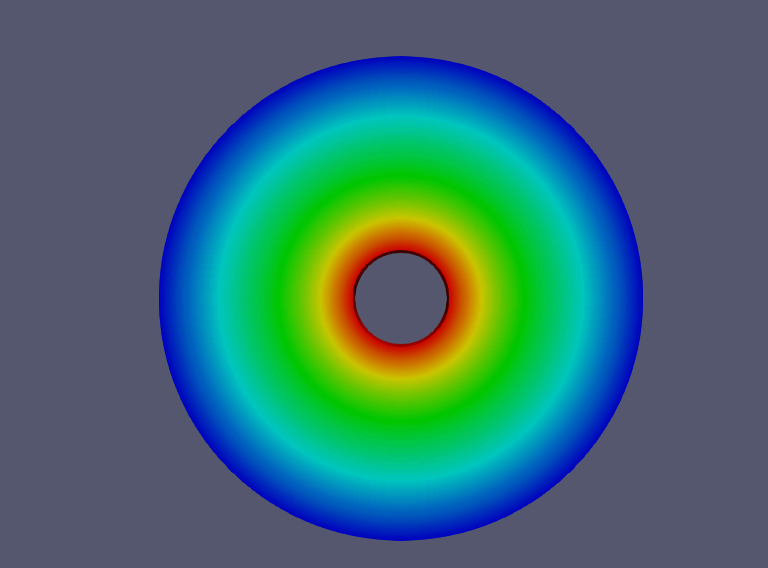
当时就被他自由面上的温度场分布震惊了,怎么是五彩斑斓状!!!
按他的设置,OPENFOAM出来的自由面温度场是这样
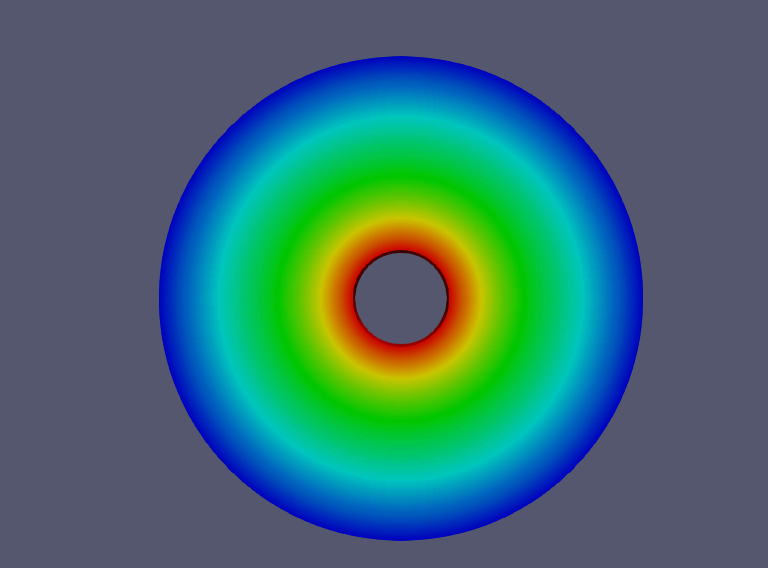
而且我昧心的感觉我这个结果还挺合理的。。。。。
更有厉害的能做出更不可思议的场分布,还能转起来http://dx.doi.org/10.1016/j.ijheatmasstransfer.2017.05.066
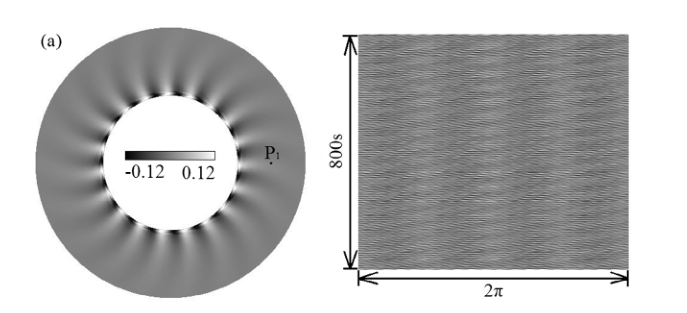
CASE实现起来很简单,无重力,用pimple算法,多了一个上自由面速度随温度梯度变化的边界条件
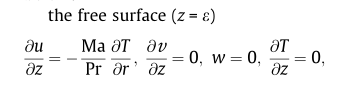
三维网格是200 40 14

case文件:传不上,求解器:也传不上。。。我微信13842091526,感兴趣的想算一下的加我啊,8核几十分钟就出结果
-
这是按照文献给出的边界条件
tmp<vectorField > marangoniFvPatchVectorField::snGrad() const { return this->patch().deltaCoeffs()*(*this - patchInternalField()); } // Evaluate the field on the patch void marangoniFvPatchVectorField::evaluate() { //Info << "entering marangoniFvPatchVectorField::evaluate()" << endl; if (!this->updated()) { //Info << "marangoniFvPatchVectorField::evaluate(): calling updatecoeffs" << endl; this->updateCoeffs(); } vectorField nHat = this->patch().nf(); vectorField pif = this->patchInternalField(); scalarField deltas=this->patch().deltaCoeffs(); fvPatchField<vector> gradT =this->patch().lookupPatchField<volVectorField, vector>("gradT"); vectorField gradT_internal = gradT.patchInternalField(); vectorField gradTplane= transform(I - sqr(nHat),gradT_internal); vectorField pifplane= transform(I - sqr(nHat),pif); fvPatchField<vector> gradC =this->patch().lookupPatchField<volVectorField, vector>("gradC"); vectorField gradC_internal = gradC.patchInternalField(); vectorField gradCplane= transform(I - sqr(nHat),gradC_internal); vectorField result=pifplane+(tmarangonicoeff_*gradTplane+cmarangonicoeff_*gradCplane)/deltas; vectorField::operator= ( result ); transformFvPatchVectorField::evaluate(); }