关于negSumDiag()的一个问题

mengweilm425

在看关于negSumDiag()的代码的时候遇到一个问题。diag上面的项是由该“行”上面的的off-diag的项相加后取负值得到。为什么下面的代码感觉像是把该“列”的数相加了呢？

template<class Type, class DType, class LUType>
void Foam::LduMatrix<Type, DType, LUType>::negSumDiag()
{
    const Field<LUType>& Lower = const_cast<const LduMatrix&>(*this).lower();
    const Field<LUType>& Upper = const_cast<const LduMatrix&>(*this).upper();
    Field<DType>& Diag = diag();

    const unallocLabelList& l = lduAddr().lowerAddr();
    const unallocLabelList& u = lduAddr().upperAddr();

    for (label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Lower[face];
        Diag[u[face]] -= Upper[face];
    }
}

以这个网格为例

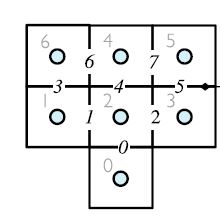
lowerAdd 为 (0 1 2 1 2 3 4 3 )
upperAdd 为 (2 2 3 6 4 5 6 5 )

矩阵的形式为

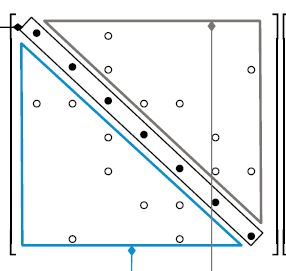
那么Diag[0] 应该是由 Upper[1]得到。这个和上面的代码不符。如果矩阵是对称的，这个计算没有问题。而如果是非对称的，是不是就有问题了？

谢谢大家！

mengweilm425

为了进一步测试，建立一个3X3的网格，并创建一个fvMatrix。

        fvVectorMatrix UEqn_lap
        (
          fvm::laplacian(nu, U)
        );

网格编号如下：

|6|7|8|
|3|4|5|
|0|1|2|

输出 upper 和lower 的address，没有问题

        Info<< "UEqn_lap upper add before sum   " << UEqn_lap.lduAddr().upperAddr() << nl << endl;
        Info<< "UEqn_lap lower add before sum   " << UEqn_lap.lduAddr().lowerAddr() << nl << endl;
UEqn_lap upper add before sum
12
(
1
3
2
4
5
4
6
5
7
8
7
8
)


UEqn_lap lower add before sum
12
(
0
0
1
1
2
3
3
4
4
5
6
7
)

下面把upper lower 和diag重新赋值并输出

        UEqn_lap.upper() = 100;
        UEqn_lap.diag() = 0;
        UEqn_lap.lower() = 1;

        Info<< "UEqn_lap diag after change   " << UEqn_lap.diag() << nl << endl;
        Info<< "UEqn_lap upper after change   " << UEqn_lap.upper() << nl << endl;
        Info<< "UEqn_lap lower after change   " << UEqn_lap.lower() << nl << endl;

输出为：

UEqn_lap diag after change   9{0}

UEqn_lap upper after change   12{100}

UEqn_lap lower after change   12{1}

调用

        UEqn_lap.negSumDiag();

        Info<< "UEqn_lap diag after negSumDiag   " << UEqn_lap.diag() << nl << endl;

输出结果为：

UEqn_lap diag after negSumDiag   9(-2 -102 -101 -102 -202 -201 -101 -201 -200)

我特意把upper里面的数值设的很大，从输出的结果看，diag 是把lower里面的数加和了，也就是把列中的数加和了。

这个结果让我有点儿弄不明白。

wwzhao

@mengweilm425 这个问题cfd-online上也有人讨论过，不过没有结果。我个人觉得这确实是OpenFOAM的bug，不过由于fvm离散后的系数矩阵的特殊性质，列元素相加和行元素相加得到的结果是一样的，因此这个bug不影响计算。有机会细说。

mengweilm425

@wwzhao 谢谢您的回复！

我找到了这个帖子

http://www.cfd-online.com/Forums/openfoam-programming-development/72456-matrix-storage-diagonal-coeffients-calculation.html

但是也没说清楚。不过系数矩阵是对称的话，确实不影响结果。

gyzhangqm

这个问题困扰我了一天，但我解决了这个问题。
首先，我们应该明白OpenFOAM中并没有存A[][]这样的系数矩阵，存的是diag，lower和upper这些非零的系数。
其次，我们在看一些教程的时候，为了解释lduAddressing中的lower(), upper(), lowerAddr(), and upperAddr(),可能把lower解释成了
the coefficient multiplying $\phi_{owner} $ in the algebraic equation for element neighbour,把upper解释成了
the coefficient multiplying $\phi_{neighbour} $ in the algebraic equation for element owner.
甚至有些教程给出了下面的解释

A[upperAddr[k]][lowerAddr[k]]=lower[k]
A[lowerAddr[k]][upperAddr[k]]=upper[k]

如果这样理解的话，当然negSumDiag是对列求和的，这和我们认知里矩阵的一行代表一个方程相违背。有人强行解释对于扩散方程因为矩阵对称，虽有对行求和对列求和结果一致。

但事实上出现这样认知的原因在于我们对lower和upper的理解出现的错误。Hrvoje Jasak在帖子中也说明了这点
https://www.cfd-online.com/Forums/openfoam-programming-development/72456-matrix-storage-diagonal-coeffients-calculation.html

经过对guassConvectionScheme的探究及对对流方程离散化的推导（原谅我尚未掌握这个论坛上使用公式排版的方法），正确的理解方式应该是：

lower存的系数代表了以Neighbour为单元的代数方程中，Owner的物理量的贡献
upper 存的系数代表了以Owner为单元的代数方程中，Neighbour的物理量的贡献

并且根据对流方程离散化的推导，我们其实可以知道diag的系数，并非为该行off-diagonal系数的和。而应该为
$$
a_C=-\sum_{f:nb(C)}{a_N}+\sum_{f:nb(C)}{\dot m_f}
$$
基于规则正交网格的推导可以参考
《The Finite Volume Method in Computational Fluid Dynamics An Advanced Introduction with OpenFOAM and Matlab》

如果有时间，我会重新排版这条回复。有任何问题可以和我联系讨论。

李东岳

感谢大佬们分享

wwzhao

@gyzhangqm

$$
a_C=-\sum_{f:nb(C)}{a_N}+\sum_{f:nb(C)}{\dot m_f}
$$

上面这个式子是不是漏了 $\phi_C$ 和 $\phi_N$？$\dot m_f$ 是不是指的 Ax=b 中的 b？

我的理解应该是

$$
a_C\phi_C = - \sum_{f:nb(C)}a_N\phi_N + b_C
$$

以上公式为计入边界条件后的表达式， $b_C$ 不为 0，且 $a_C$ 的值被边界条件影响。

negSumDiag 只对 diag， lower 和 upper 做了操作，并没有计入边界条件的影响，所以其过程并不对应以上公式。

gyzhangqm

@wwzhao

扩散方程比较容易理解。这里仅以对流方程为例，不考虑边界条件，不考虑网格扭曲的影响。下面是我的理解。

仅考虑对流项
$$\nabla \cdot ( \rho \mathbf { u } \phi ) = 0$$
将对控制单元$O$的体积分转化为面积分，$ f \sim n b ( O )$为控制单元$O$的控制面，$N \sim NB ( O ) $为控制单元$O$的的邻居单元
$$\sum _ { f \sim n b ( O ) } ( \rho \mathbf { u } \phi ) _ { f } \cdot \mathbf { S } _ { f } = 0$$

定义
$$\dot { m } _ { f } = ( \rho \mathbf { u } ) _ { f } \cdot \mathbf { S } _ { f }$$

面心的物理量通过两侧体心物理量加权平均得到：
$$\phi _ { f } = \varpi \phi _ {O} + ( 1 - \varpi ) \phi _ { N }$$
上面公式整理后为：
$$\sum _ { f \sim n b ( O ) } ( \rho \mathbf { u } \phi ) _ { f } \cdot \mathbf { S } _ { f } = \sum _ { f - n b ( O ) } \dot { m } _ { f } \phi _ { f } = a _ { O } \phi _ { O } + \sum _ { N \sim NB ( O ) } a _ { N } \phi _ { N } = 0$$

其中
$$a _ { N } = \dot { m } _ { f } ( 1 - \varpi ) _ { f }$$
$$a _ { O } = \sum _ { f \sim n b ( O ) } \dot { m } _ { f } \varpi = - \sum _ { N \sim NB ( O ) } a _ { N } + \sum _ { f \sim n b ( O ) } \dot { m } _ { f }$$

在gaussConvectionScheme<Type>::fvmDiv中

    fvm.lower() = -weights.primitiveField()*faceFlux.primitiveField();
    fvm.upper() = fvm.lower() + faceFlux.primitiveField();
    fvm.negSumDiag();

可以看出，lower存的是 $- \varpi _ { f } \dot { m } _ { f } $，代表了以Neighbour为单元的代数方程中，Owner的物理量$\phi _ { O }$的贡献 ,upper 存的是$\dot { m } _ { f } ( 1 - \varpi ) _ { f } $，代表了以Owner为单元的代数方程中，Neighbour的物理量$\phi _ { N }$的贡献。这里所说的Neighbour和Owner，其实是立足于面的，Owner是该面左侧的单元，Neighbour是该面右侧的单元，Owner编号小于Neighbour编号。

至于weights的具体计算，则根据具体的插值格式进行计算，对于Upwind、FROMM、QUICK，TVD等不同格式，分别有不同的计算方法，这里暂不讨论。

这里有个trick，$a _ { N } = \dot { m } _ { f } ( 1 - \varpi ) _ { f }$，为什么对于编号大于Owner的邻居单元，upper 存的是$\dot { m } _ { f } ( 1 - \varpi ) _ { f } $，而对有编号小于Owner的邻居单元，lower存的是 $- \varpi _ { f } \dot { m } _ { f } $呢?这是因为计算面心的系数$\varpi$时在总是认为面左侧是Owner，右侧是Neighbour.

最后是 fvm.negSumDiag()求和计算对角项的系数$a _ { O } $。这里我们并非按照公式$a _ { O } = \sum _ { f \sim n b ( O ) } \dot { m } _ { f } \varpi$，先对所有的cell循环，然后对每个cell的所有面循环，这样计算效率底下，非结构网格程序一般都是对所有的面进行循环，将其贡献分别计入两侧的控制体中。

    for (label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Lower[face];
        Diag[u[face]] -= Upper[face];
    }

这里是对列求和，而非对行求和。如果是对行求和的话，得到的是$- \sum _ { N \sim NB ( O ) } a _ { N }$。而对角项的系数$a _ { O } = - \sum _ { N \sim NB ( O ) } a _ { N } + \sum _ { f \sim n b ( O ) } \dot { m } _ { f }$.

那么最后的问题就是为什么对列求和得到的是正确的$a _ { O } = - \sum _ { N \sim NB ( O ) } a _ { N } + \sum _ { f \sim n b ( O ) } \dot { m } _ { f }$，这是巧合么？并不是巧合，而是必然。仔细想想这些系数所代表的含义，

lower存的系数代表了控制面右侧的单元(Neighbour)的代数方程中，控制面左侧单元(Owner)的物理量的贡献
upper 存的系数代表了控制面左侧单元(Owner)的代数方程中，控制面右侧的单元(Neighbour)的物理量的贡献

另一方面在$\mathbf A\phi=\mathbf b$中

矩阵$A$中的第$i$行的非对角项系数，其实代表了与编号为$i$的单元相邻的单元物理量对$i$的单元控制方程的贡献。
矩阵$A$中的第$j$列的非对角项系数，其实代表了编号为$j$的单元对其相邻的单元控制方程的贡献。

对于对流项，单元$i$对单元$j$的影响不等于单元$j$对单元$i$的影响，但是，编号为$j$的单元对所有与其相邻的单元的贡献的总和，正应该是$j$的单元自身系数的相反数。也正是矩阵$A$中的第$j$列的非对角项系数之和的相反数。

以上理解也只是我个人根据guassConvectionScheme.C文件的自我解读。如果哪里有理解错的地方，还请指正。

wwzhao

@gyzhangqm

很精彩的推导！解开了我一直以来的疑惑。

不过有一点我不认同：

这里有个trick，$a _ { N } = \dot { m } _ { f } ( 1 - \varpi ) _ { f }$，为什么对于编号大于Owner的邻居单元，upper 存的是$\dot { m } _ { f } ( 1 - \varpi ) _ { f } $，而对有编号小于Owner的邻居单元，lower存的是 $- \varpi _ { f } \dot { m } _ { f } $呢?这是因为计算面心的系数$\varpi$时在总是认为面左侧是Owner，右侧是Neighbour.

这里的trick（正负号）应该是求flux的时候设置的，而不是求weight。

我换个说法理一下思路：

对于单元 $P$，有 $k$ 个面，也就有 $k$ 个邻居单元，记为 $N_1$ ... $N_k$。

每个面心的量通过面的 owner 和 neighbour 单元体心插值得到（注意这里的 owner、neighour 和上面的 $P$、$N$ 完全不相关，为了避免歧义，上面的单元用 $P$ 而不是用 $O$ 表示）

$$
\phi_ f = \varpi \phi_{own} + (1 - \varpi) \phi_{nei}
$$

于是对流项的积分变为

$$
\sum_{f=1}^{k} (\rho \mathbf { u } \phi) _ {f} \cdot \mathbf S_f = \sum_{f=1}^k \dot m_f \phi_f
$$

上式中的 $\dot m$ 为质量通量，这个是由速度点乘面法向得到的。具体操作为 fvc::flux(U)，也就是 mesh.Sf() 和 U 的点乘。Sf() 是一个矢量场，它的方向很有讲究。它被规定为从 own 指向 nei。而高斯定理的 $\mathbf S_f$ 规定方向指向封闭单元外。这两个定义是由矛盾的。因此需要上面的trick来调整正负号。

先看非对角元素。遍历 P 的所有面单元：

若该面单元的 own 为 P， nei 为 N，Sf() 与 $\mathbf S_f$ 同方向
这种情况下，N 的系数在 upper，因此 upper 需要加上 $\dot m(1 - \varpi)$。同时 P 的主对角元素加上 $\dot m \varpi$。
若该面单元的 nei 为 P，own 为 N，Sf() 与 $\mathbf S_f$ 反方向
这种情况下，N 的系数在 lower，原本 lower 需要加上 $\dot m \varpi$，调整负号后，最终加上的是 $-\dot m \varpi$。同时 P 的主对角元素加上 $-\dot m(1 - \varpi)$。

以上过程对应以下两行代码：

    fvm.lower() = -weights.primitiveField()*faceFlux.primitiveField();
    fvm.upper() = fvm.lower() + faceFlux.primitiveField();

再看主对角元素。

对于邻居单元 N ，在计算其对应行的非对角系数时，所用插值公式和 P 相同，即还是

$$
\phi_ f = \varpi \phi_{own} + (1 - \varpi) \phi_{nei}
$$

也就是说以上公式要用两次，分别是在 P 和 N 作为主对角元素的行上使用。

在循环到 N 与 P 共享的面单元时：

若该面单元的 own 为 P， nei 为 N，Sf()方向为 P->N ，$\mathbf S_f$ 方向为 N->P，二者反方向
这种情况下，P 的系数为 $-\dot m \varpi$。
若该面单元的 nei 为 P，own 为 N，Sf() 方向为 N->P， $\mathbf S_f$ 方向也为 N->P，二者同方向
这种情况下，P 的系数为 $\dot m(1 - \varpi)$ 。

注意以上两种情况，P 作为 N 的非对角系数和作为其本身的主对角系数正好是相反数，且处于同一列上。由于遍历一次面单元将所有网格单元（包括P和其所有邻居单元）的非对角元素都计算好了，为了避免重复计算，所以直接用该列的非对角元素加和并取相反数得到主对角元素的值。

即对应代码：

    fvm.negSumDiag();

也就是说 negSumDiag 计算的确实是列，而不是行。我之前会由系数矩阵对称的错觉是因为采用的验证算例都是采用线性插值计算面心物理量，这使得插值系数 $\varpi=0.5$，正好造成系数矩阵反对称的假象。

李东岳

插一句：我觉得CFD教材应该把结构网格简化，着重讨论非结构网格。另外， @wwzhao 的讨论把$P$，$N$省略的替换为通量正负看起来更简洁，因为已经有own与nei的标识了。

不管怎样，惊为天人大佬们继续！！

gyzhangqm

@wwzhao

是的,OpenFOAM中面的方向定义永远是从小编号指向大编号，Gauss定理中面的方向指向外。也许把这些面分为大面和小面区分一下更容易理解。

对于编号大于$P$的单元$U$,他们之间面上的量为:

$$\phi_ f = \varpi \phi_{P} + (1 - \varpi) \phi_{U}$$

$$\dot { m } _ { f } = ( \rho \mathbf { u } ) _ { f } \cdot \mathbf { S } _ { f }$$

对于编号小于$P$的单元$L$,他们之间面上的量为:

$$\phi_ f = (1 - \varpi) \phi_{P} + \varpi\phi_{L}$$

$$\dot { m } _ { f } =- ( \rho \mathbf { u } ) _ { f } \cdot \mathbf { S } _ { f }$$

$$
\sum _ { f \sim n b ( P ) } ( \rho \mathbf { u } \phi ) _ { f } \cdot \mathbf { S } _ { f }
= \sum _ { N \in L ( P ) } \left( - \dot { m } _ { f } \phi _ { f } \right) + \sum _ { N \in U ( P ) } \dot { m } _ { f } \phi _ { f }
$$
$$
= \sum _ { N \in L ( P ) } - \dot { m } _ { f } \left[ ( 1 - \varpi ) \phi _ { P } + \varpi \phi _ { N } \right] + \sum _ { N \in U ( P ) } \dot { m } _ { f } \left[ \varpi \phi _ { P } + ( 1 - \varpi ) \phi _ { N } \right]
$$

$$
= \left( \sum _ { N \in L ( P) } - \dot { m } _ { f } ( 1 - \varpi ) + \sum _ { N \in U ( P ) } \dot { m } _ { f } \varpi \right) \phi _ { P } + \sum _ { N \in L ( P ) } - \dot { m } _ { f } \varpi \phi _ { N } + \sum _ { N \in U ( P ) } \dot { m } _ { f } ( 1 - \varpi ) \phi _ { N }
$$

这样可以看出lower存的是 $- \varpi _ { f } \dot { m } _ { f } $, upper存的是$\dot { m } _ { f } ( 1 - \varpi ) _ { f } $.并且diag存的是
$$a _ { P } = -[\sum _ { N \in L ( P ) } \dot { m } _ { f } ( 1 - \varpi ) + \sum _ { N\in U ( P ) } (-\dot { m } _ { f } \varpi )]$$

CFD中文网

关于negSumDiag()的一个问题