为什么网格质量会影响收敛?
-
做CFD模拟时,通常我们在划分完网格后会检查一些标志网格质量的参数,如正交性,膨胀比还有skewness等,在计算时质量高的网格往往会更容易得到收敛的解。
但网格质量到底是如何影响收敛的呢?就最后生成的线性系统而言,差的网格和好的网格,其具体影响的是哪一部分呢?
先行谢过各位的答疑解惑! -
比如正交性,有时候不用正交修正,在结果中会出现很大的耗散,当然网格也不是越细越好,有的时候中等网格得到的结果会更好~,一些湍流模型的内部参数对于网格的尺度有要求,这个大家都知道,但是这个尺度是多少,很多是不同的研究对象还是不一样的,这个就好比装大运,有的就非常不符合常理,就比如LES都是比RANS好,但是有时候RANS的到的结果和实验相比可能相对于LES更快,物理现象更符合;
针对大多数网格是按照前人总结的,但是有时候自己的研究对象还是要和实验对比,这就是为啥论文中,评审专家都要看实验状况,而不是全部分仿真,毕竟有时候,一些东西,就是和我们想的不一样
-
@paopaoai11 有限体积法求解过程有很多假设,最基本的网格假设是均匀正交棋盘形,这也是最简单的情形,比如陶文铨老师的《数值传热学》、王福军老师的《计算流体动力学分析》推导基本的流场数值计算时,就是用这种简单情况推导,网格界面处的值又是通过线性插值插出来的,误差直接跟网格尺度和节点位置相关,同时流动不一定都沿着网格方向,尤其是压力梯度等变量,这可能导致不合理的压力波等问题,然后就有了交错网格、同位网格等等发展,但这仍然很简单,对实际流动仍然不够,后边又发展出非结构网格,这时候控制方程的离散,不但跟网格节点位置、网格尺度相关,还跟网格界面外法线矢量方向有关,流动方程的误差就跟计算各种矢量角度产生了关联,但计算机有截断误差之类的影响,最后反映到流动计算上,这些网格面之间的角度就是所谓的正交性、膨胀比之类的,就直接影响计算精度。
-
在评估网格质量的时候,一般常用下面4种标准进行衡量。
1 均匀性(Uniformity)
定义:网格从最小单元过渡到最大单元的速度(反之亦然)。
网格单元之间尺寸变化越缓慢,则均匀性越好,结果越精确。
一般来说,当整个计算域空间的所有网格都在同一尺寸时,均匀性是最好的。然而,在一些区域,所允许的最大网格尺寸非常小,因此,如果在整个计算域都采用这种尺度的网格将会导致过多的网格数目,这在实际应用中是不现实的。
有了这个约束,在网格划分阶段,决定从哪里开始进行网格单元增长,以多大的速率增长就非常重要了,最终目的是在保证关键位置网格解析度的同时尽可能减少总的网格数目。2 纵横比(aspect ratio)
定义:下面两个值中较大的一个:
• 网格单元边界框各个面中最大面积和最小面积的比值
• 表达式的值:
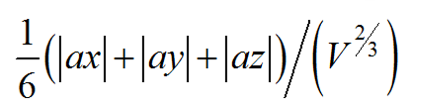
其中,ax、ay、az是网格单元边界框各个面的面积,V是网格单元的体积
纵横比越接近1,结果越精确。
这类网格质量问题最常见于两种情景:
• 边界层网格
• 六面体网格的各向异性细化(refinement)
前者最为常见,为了捕捉近壁面处流动,需要在垂直壁面方向上布置非常精细的网格,尤其对于Yplus≈1的情形,有可能会导致纵横比高达几千。
后者常见于网格加密,譬如在模拟船体兴波时,对于自由液面处网格的加密,将导致垂向上的网格尺度远远小于纵向上的尺度。3 正交性(Orthogonality)
定义:连接两个相邻单元中心的直线和两个单元所共面的法线之间的夹角。
越接近于0,精度越高。
在多面体网格中,正交性经常被提及,因为在有限的空间中,网格单元的形状可以有多种选择。正交性对于模拟精度具有重要影响,因为它与变量梯度、粘性和对流通量的计算息息相关。4 偏斜度(Skewness)
定义:连接相邻两个单元中心的直线与所共面的交点,距离该面中心点的长度。
偏斜度越接近于0,精度越高。
较为复杂的几何结构加上比较粗糙的网格,是导致偏斜度大的主要罪魁祸首。同样,该因素对于结果的精确性也有很大影响,它影响着通量平衡的计算。
针对此因素,提高网格质量的方法一般是在几何较为复杂的地方,适当减小网格尺寸和增加网格密度。
