气液流动过程中温度直接求解问题
-
目前在求解两相可压缩流动过程时的温度方程时出现一些问题,请教一下各位老师前辈。求解发现,管道内流体流到处温度急剧下降至0.01K量级,直至发散。试图将不同相除以其密度再相加,问题依旧存在,感觉方程和植入没啥问题,不知道为啥始终求得温度接近0K,烦请各位老师指点一二,谢谢!
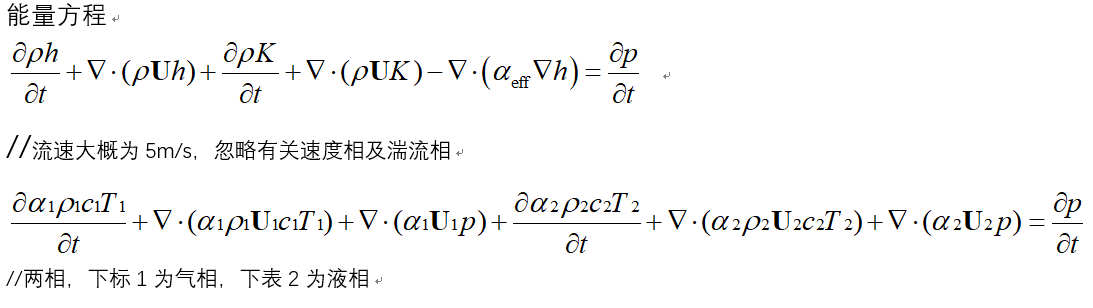
alphacp1 = alpha1*cp1*rho1; alphacp2 = alpha2*cp2*rho2; alphaphicp1 = fvc::interpolate(alphacp1*U1) & mesh.Sf(); alphaphicp2 = fvc::interpolate(alphacp2*U2) & mesh.Sf(); surfaceScalarField birho1 = fvc::interpolate(alpha1*rho1*U1) & mesh.Sf()/fvc::interpolate(rho1); surfaceScalarField birho2 = fvc::interpolate(alpha2*rho2*U2) & mesh.Sf()/fvc::interpolate(rho2); fvScalarMatrix TEqn ( fvm::ddt(alphacp1,T) + fvm::ddt(alphacp2,T) + fvm::div(alphaphicp1,T) + fvm::div(alphaphicp2,T) + fvc::div(birho1,p) + fvc::div(birho2,p) - fvc::ddt(alpha1,p) - fvc::ddt(alpha2,p) ); TEqn.solve(); -
@李东岳 东岳老师,上次温度方程求解错误主要是由于两个原因,一个是边界条件给错了,还一个是温度方程和动量、连续相方程耦合求解了,经过更改已经可以正常运行。但目前在验证算例时发现和实验值存在较大的误差。
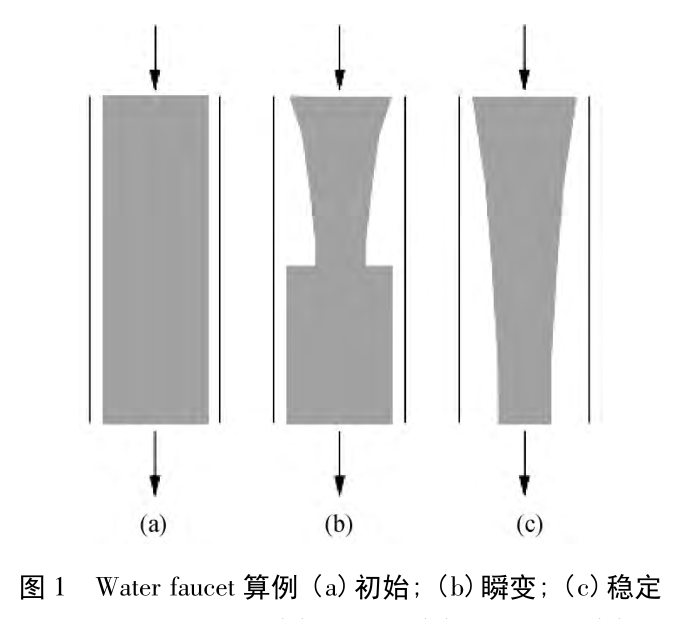
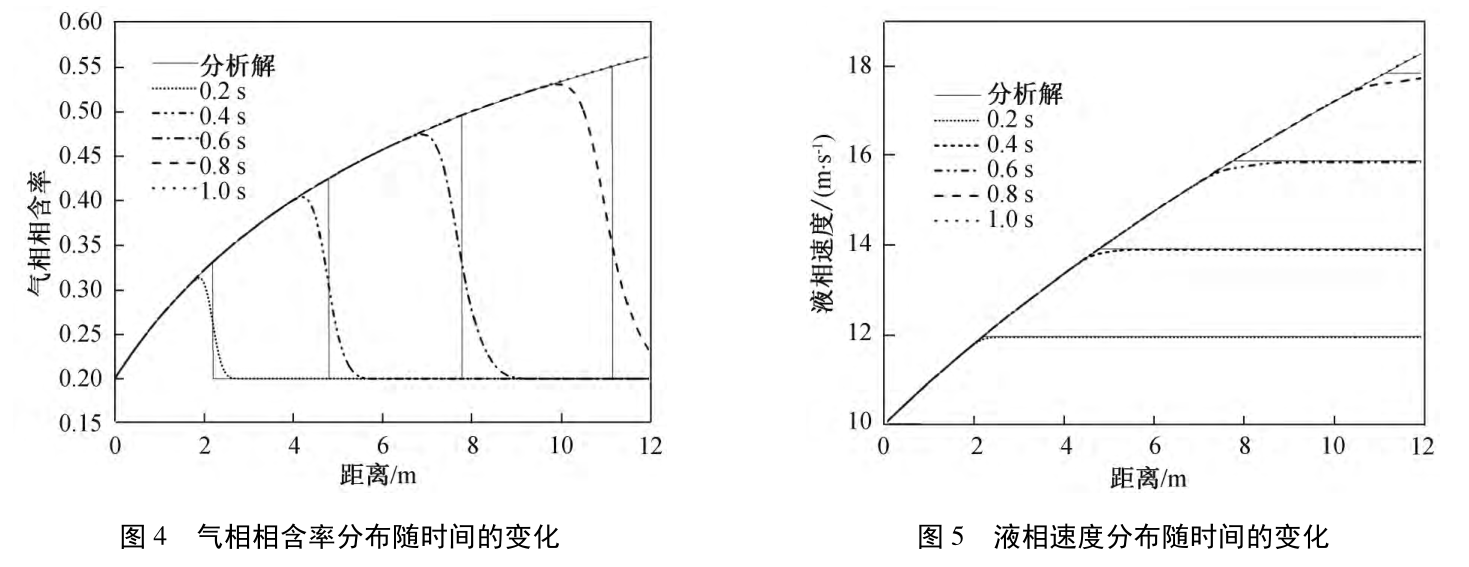
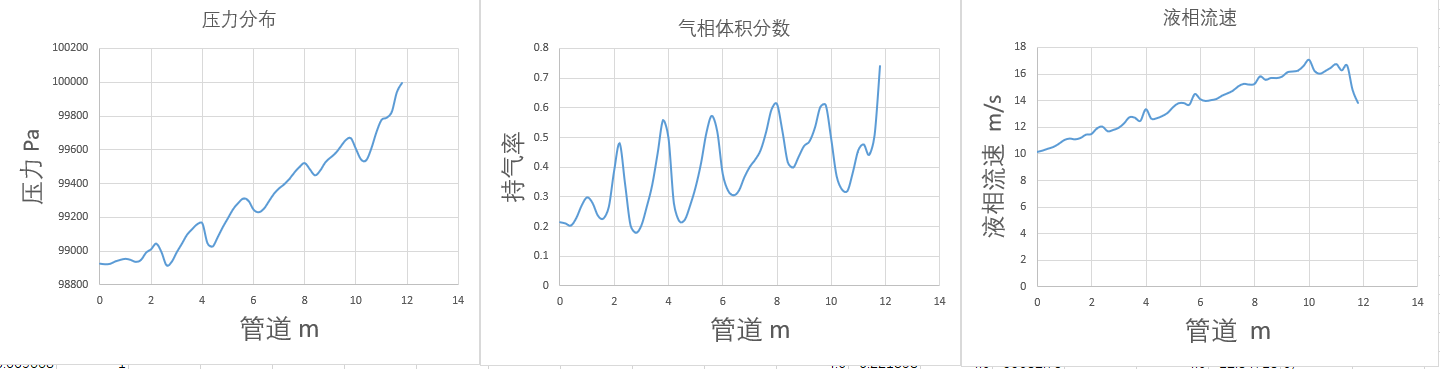
验证算例如下: 一根长为 12 m, 直径为 1 m的垂直管, 管道上端为入口, 管道下端为出口,出口压力是 1e5Pa, 气液相分别为空气和水,温度均为 25 ℃ .入口处 x = 0, 出口处 x = 12 m.初始状态如图 1(a)所示, 气相相含率 0. 2, 气相速度 Vg=0;液相相含率 0. 8, 液相速度 Vl=10 m/s。使用双欧拉求解。耦合求解动量及连续性方程(参考瞬态可压缩压力泊松方程),收敛后求解相率方程,进行下一时间步。图一是示意图,图二是解析解的气相分数及液相流速,图三为求解出的压力、持气率、液相流速,可以看出波动很大,尤其持气率波动尤其大,已经排除网格密度的原因。能力有限,查找一周的错误了,实在找不到什么别的原因了,还望东岳老师和前辈指点一二。
气液相动量方程:fvVectorMatrix UEqn1 ( fvm::ddt(alpharho1, U1) + fvm::div(alphaphi1, U1) == -pGrad1-Sg ); UEqn1.solve(); fvVectorMatrix UEqn2 ( fvm::ddt(alpharho2, U2) + fvm::div(alphaphi2, U2) == -pGrad2-Sl ); UEqn2.solve();连续性方程
psi1 = 1/Cg/Cg; psi2 = rho2/p; volScalarField rAU1(1.0/UEqn1.A()); surfaceScalarField rhorAUf1("rhorAUf1", fvc::interpolate(alpharho1*rAU1/rhog)); volVectorField HbyA1(constrainHbyA(rAU1*UEqn1.H(), U1, p)); surfaceScalarField phiHbyA1 ( "phiHbyA1", ( fvc::interpolate(psi1*alpha1/rhog) *fvc::flux(HbyA1) ) ); volScalarField alphapsi1("alphapsi1",alpha1*psi1/rhog); volScalarField rAU2(1.0/UEqn2.A()); surfaceScalarField rhorAUf2("rhorAUf2", fvc::interpolate(alpharho2*rAU2/rho2)); volVectorField HbyA2(constrainHbyA(rAU2*UEqn2.H(), U2, p)); surfaceScalarField phiHbyA2 ( "phiHbyA2", ( fvc::interpolate(psi2*alpha2/rho2) *fvc::flux(HbyA2) ) ); volScalarField alphapsi2("alphapsi2",alpha2*psi2/rho2); fvScalarMatrix pEqn ( fvm::ddt(alphapsi1, p) + fvm::ddt(alphapsi2, p) + fvm::div(phiHbyA1, p) + fvm::div(phiHbyA2, p) - fvm::laplacian(rhorAUf1, p) - fvm::laplacian(rhorAUf2, p) ); pEqn.solve(); rho1 = p*psi1; rho1.correctBoundaryConditions();surfaceScalarField phi1 = fvc::interpolate(rho1*U1) & mesh.Sf(); surfaceScalarField phi2 = fvc::interpolate(rho2*U2) & mesh.Sf(); fvScalarMatrix alpharhoEqn1 ( fvm::ddt(rho1,alpha1) + fvm::div(phi1,alpha1) ); fvScalarMatrix alpharhoEqn2 ( fvm::ddt(rho2,alpha2) + fvm::div(phi2,alpha2) ); alpharhoEqn1.solve(); alpharhoEqn2.solve(); alpha1 = alpha1/(alpha1+alpha2); alpha2 = 1 - alpha1; alpha2.correctBoundaryConditions();




