通过流场和矩方法计算颗粒物的问题
-
各位老师、各位前辈好:
最近在通过CFD和MOM计算颗粒物浓度的时候遇到了一些问题和困惑,希望有前辈、老师能够指点一下。
首先这个模型仅考虑了颗粒物的沉积损失,不考虑成核等过程。

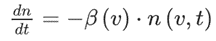
然后通过对数正态分布矩方法把这个GDE方程写出矩的形式,如下:(下面分别是i=2和i=2.6的情况下)
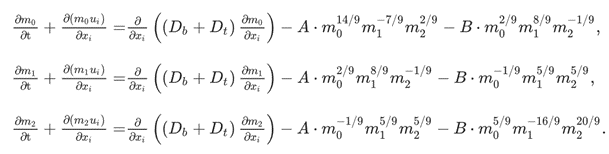
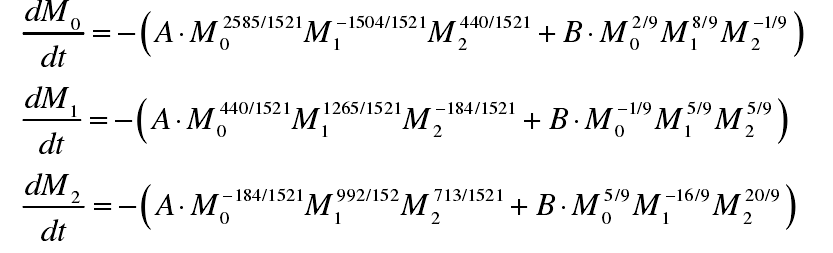
为了确保准确,我先照着文献数值计算了一下相关内容:(包括沉降率、粒径分布变化等等)
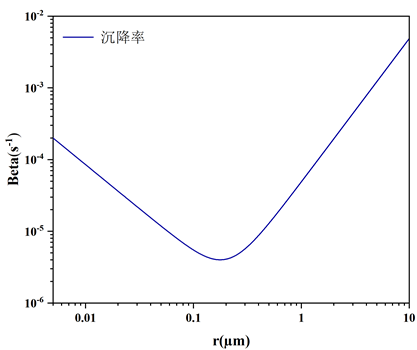
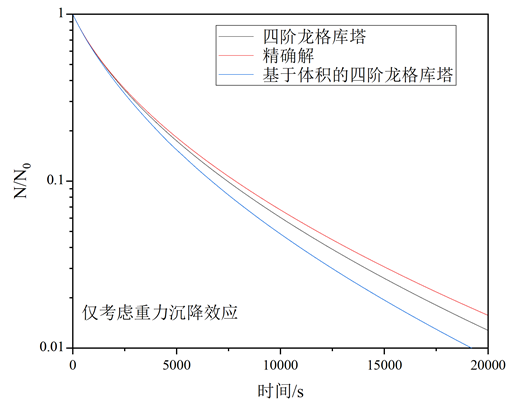
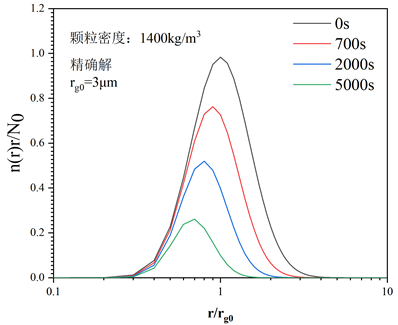
然后这个仅考虑了前三阶矩,矩的初始值由下面的式子进行计算,分别是用平均体积和平均半径计算,这就出现了第一个问题,这两个计算公式算出来的矩初始值不一样。我再确保跟文献的结果没太大差别后,进行了下一步工作,就是通过Fluent中的UDF将这个颗粒物沉降编写为源项,将三阶矩分别编写成三个UDS方程来进行求解。但是在求解时候发现老是发散,然后基于平均体积、i=2和i=2.6计算的时候,发现M1和M2总是变成了负数,或者M1也是负数。


下面是计算的一些图片,


下面是M0、M1和M2的残差变化,这个一看就有问题
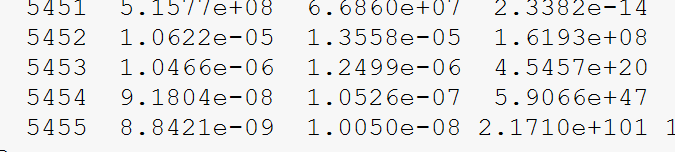
因此,想跟各位老师请教一下这个问题,首先是为什么这两个公式算出来的矩初值不一样,然后就是发散的问题,我想请教下这么用UDF进行计算是正确的么,流场和MOM共同求解的话正确解法是什么样的。 -
矩量计算公式是决定式,不是定义式。就是说不是矩量被定义成等于那个。之所以写成等于那个是有前置的决定条件。
你写的两个公式,左边那个是经典矩方法中常用的,能写成这样是有个前提条件:该粒子群已经处于对数正态分布,且对数正态分布的表达式为[1]中(23)式。(因为对数正态分布有7种,所以要指定形式)
右边那个我不认识...

只有有了这样的前提条件,才能给出各阶矩量的表达式是什么。可以看文献 [1] 里 (23) 到 (28) 的过程。
还有,你的计算好像没有无量纲化。这也很可能会引起问题。文献 [1] 里的 table 1 有无量纲过程。
[1]PRATSINIS S E. Simultaneous nucleation, condensation, and coagulation in aerosol reactors[J/OL]. Journal of Colloid and Interface Science, 1988, 124(2): 416-427. DOI:10.1016/0021-9797(88)90180-4.
-
@bestucan 是的老师,我这个是对数分布的矩方法不是TEMOM,我是看了文献[1]他用的这个经典矩方法和TEMOM处理这个颗粒物沉积计算的,右边的表达式是在文献[2]中看见的。然后,老师这个无量纲化我算三维的也是需要先把变量都无量纲化,然后解三个三维的无量纲标量方程么。
感谢老师的解答,我看看这个文献具体操作
[1]Guangping Xu, Jiasong Wang,CFD modeling of particle dispersion and deposition coupled with particle dynamical models in a ventilated room. DOI:https://doi.org/10.1016/j.atmosenv.2017.07.027.
[2]S.H. Park, K.W. Lee,Analytical solution to change in size distribution of polydisperse particles in closed chamber due to diffusion and sedimentation. DOI:https://doi.org/10.1016/S1352-2310(02)00673-8.


