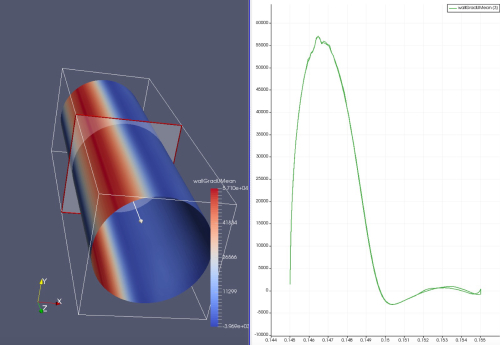
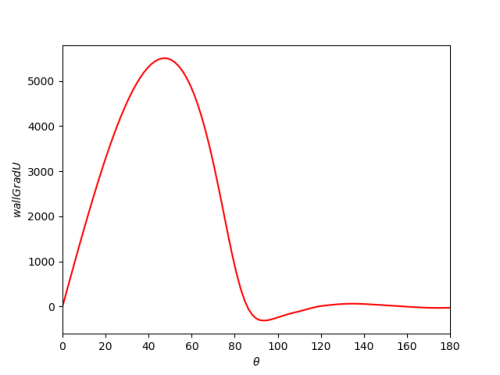
Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam
-
再仔细分析了一下计算,代码,和计算结果,又产生了疑惑。
疑惑的对象是: 二阶张量点乘(内积,dot product)一个矢量,其结果应该还是一个矢量。这个点乘与两个矢量之间的点乘不太一样。后者结果是一个数。其物理意义是一个矢量在另外一个矢量方向上的投影长度乘以被投影到的这个矢量的模长。
那么这里的二阶张量点乘一个矢量得到的这个新矢量代表着什么呢?
这个新的矢量是否代表这着 du/dn, dv/dn 以及dw/dn?
那这个新矢量的物理意义就是某个点的速度沿法向量方向上的梯度?并不是我们要求的速度沿圆周面切线的分量沿法向量的梯度?
越绕越糊涂。
-
@random_ran 之前我的表述有误。这里不涉及到二阶张量,snGrad返回的是一个矢量,代表壁面处速度沿法向的变化率。由于壁面上的速度为0,所以snGrad返回的实际上就是第一层网格的速度除以第一层网格格心到壁面的距离。snGrad是平行壁面的,在二维情况下(+x为右,+y为上,流速指向+x),取圆周上半部分,当snGrad的方向由顺时针变为逆时针时(snGrad在顺时针切向方向的投影符号发生变化),即为流动分离点。
-
再顺思路:
-
将速度(矢量)沿切线(矢量)分解,求出切线速度(矢量)
-
对1所得切线速度(矢量)求梯度,得到含九个分量的二阶张量
-
用这个张量点乘法向量得到一个新的矢量,也就是切线速度沿法线上的梯度
-
将3中所得矢量点乘切线向量,最后得到一个标量
-
沿圆周画出4得到的标量,找到等于零的点对应的座标
这是目前基于O.F.直接计算结果,我能想到的计算分离角的方法。ParaView似乎对叉乘不太支持?这样第一步似乎就走不通了。还需要再研究。
看来不动O.F.代码真是麻烦了...
-
-
@random_ran 我改的代码如下,写的可能有点啰嗦,如果有更好的表达形式望告知
forAll(wallGradUMean.boundaryField(), patchi) { const fvPatch& currPatch = patches[patchi]; if (isA<wallFvPatch>(currPatch)) { wallGradUMean.boundaryField()[patchi] = ( -UMean.boundaryField()[patchi].snGrad() & ( ( mesh.Sf().boundaryField()[patchi] /mesh.magSf().boundaryField()[patchi] ) ^ vector(0,0,1) ) ) * sign(mesh.Sf().boundaryField()[patchi] & vector(0,1,0)); } } -
一种方法:
求出平均速度之后,用ParaView的 GradientOfUnstructuredDataSet 直接计算vorticity在Z方向上的分量. 不用动代码,只需要ParaView 5.2.0 版本以上。
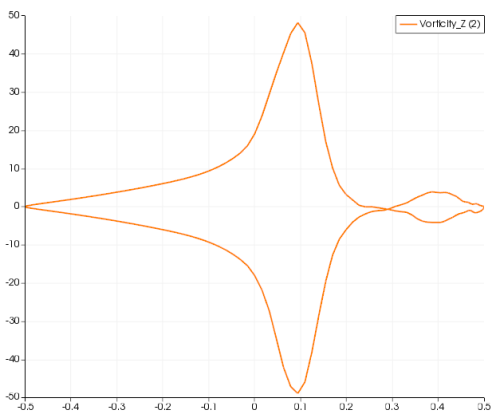
-
@random_ran 这个我也试过,还要再次处理,我觉得有点麻烦,所以改了代码,我比较懒😂
-
@random_ran 这个圆形正交网格正交性确实很好,我也是做一个圆柱绕流DNS的算例验证Re=3900,刚开始采用o型网格感觉网格质量不是很好,计算效率不是很高。想换成此篇文献中的圆形正交网格,但不知道这样的网格边界条件是怎么设定的,比如说出口,入口的边界是半圆吗?希望你能解答一下疑惑
-
@bingningmeng45
固定速度进口,零法向梯度出口,
零法向梯度压力进口,固定值压力出口。
Re=150
我参考的是一个SCI的文章,不过那个文章里面并没有解释为什么要用圆形计算域。如果单纯只是为了保证网格非正交质量,在圆形计算域外拓展为矩形不知有何影响?
http://www.sciencedirect.com/science/article/pii/S0307904X08000243
-
@bingningmeng45
一开始的时候,我是用ICEM画的网格,矩形计算域。费劲周折对于3900的Re,Cd依然给出了偏高的预测。圆形网格我是用ANSYS自带的网格生成,几乎是自动生成的。一方面质量高,另一方面操作简单,所以就没在纠结在矩形计算域为什么预测出偏高的Cd。 CFD中很重要的一步:网格无关性验证。就是说无论我用什么样形态的计算域,只要计算域足够大,随着对网格的加密,最终的数值解应该会去逼近一个值。 很明显,用圆形计算域更容易实现这个过程。
我注意到你是用DNS来算。我不知道你的计算效率不高具体不高到什么程度。你用的什么版本的O.F.,你的计算设备怎么样?至于边界条件的设置,你可以参考摩托车算例。
cd $FOAM_TUTORIALST/incompressible/pisoFoam/les/你可以试试
fixedValue或者
turbulentInlet我也用的是 @李东岳 给出的解释。
@李东岳 文献中这种圆形计算域越来越多。而且从圆形计算域衍生出来的计算域形态,比如在尾流曲渐进加密,可能能更好地捕捉尾流细节。
目前,我没有看到系统的比较计算域之间的差异,对这个经典问题的研究。还希望有了解的朋友指出。
这个网站上有人给出了这个经典算例,用网站的自己服务器两天左右就计算完成。
供你参考。