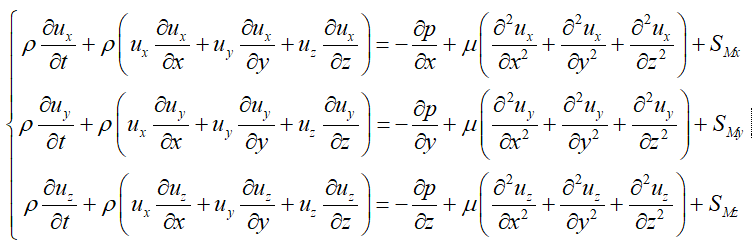请教各位老师关于动量控制方程在数值求解过程中的问题
-
请教各位老师两个问题（1）在采用有限体积法对方程进行离散之后，动量控制方程中左侧的惯性力项如何计算？
（2）在高湍流度的流动中，方程右侧的粘性力项很小，流体的受力状态如何理解？（左侧惯性力与右侧压力梯度的平衡吗？广义源项的加入如何影响流动的发展呢？） 谢谢~~~
-
速度的物质倒数两端乘以密度，再化简，就是时间项和对流项加在一起。
密度就是单位体积的质量，速度的物质导数就是加速度。
所以时间项和对流项加在一起就是单位体积内的$F=ma$，即$F=\rho a$。这就是惯性力吧？力分为体积力和表面力，本来表面力应该是产生相对于体心的力矩。但是无限小体积的情况下把力臂忽略了（我猜的），力矩造成的转动靠物理规则演化出来而不故意设计出来。所以左边是流体微元变化需要的力，右边是流体微元真实受到的力，两者相等，就推出来流体微元怎么变化的了。
物理意义有助于了解方程怎么来的，但是后来方程形式因为代换化简早没有了当初的模样，只能从大概上理解。像广义的源项，这个和运输方程放在一起好理解。NS方程化简到最后是三个运输方程，运输的物理量分别是密度、速度、熵还是啥。源项，就像一个无源封闭体内进来多少就出去多少，但是有了源，就兴许进来的少出去的多。就是对运输产生了扰动。
要是搁到动量方程上，比如加个源项，磁流体在磁场中受电磁力，或者离心机里受额外的等效重力。
另外粘性造成的应力是和速度有关系的吧？叫本构关系，用来区别牛顿和非牛顿流体的。系数小不打紧，只要湍流涡够多，速度够快。耗散能量的能力就很强。
