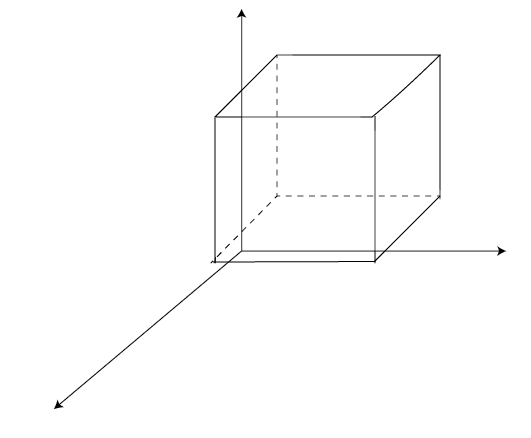
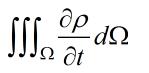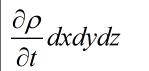连续性方程推导的疑问(微元控制体)
-
x方向流入质量:$(\rho u)|_{x} \Delta y \Delta z$
x方向流出质量:$(\rho u)|_{x+\Delta x} \Delta y \Delta z$
y方向流入质量:$(\rho v)|_{y} \Delta x \Delta z$
y方向流出质量:$(\rho v)|_{y+\Delta y} \Delta x \Delta z$
z方向流入质量:$(\rho w)|_{z} \Delta x \Delta y$
z方向流出质量:$(\rho w)|_{z+\Delta z} \Delta x \Delta y$于是,
$\frac{\partial \rho}{\partial t}\Delta x \Delta y \Delta z = ((\rho u)|_{x} - (\rho u)|_{x+\Delta x}) \Delta y \Delta z + ((\rho v)|_{y} - (\rho v)|_{y+\Delta y}) \Delta x \Delta z + ((\rho w)|_{z} - (\rho w)|_{z+\Delta z}) \Delta x \Delta y$两边除以 $\Delta x \Delta y \Delta z$
$\frac{\partial \rho}{\partial t} = \frac{(\rho u)|_{x} - (\rho u)|_{x+\Delta x}}{\Delta x} + \frac{(\rho v)|_{y} - (\rho v)|_{y+\Delta y}} {\Delta y} + \frac{(\rho w)|_{z} - (\rho w)|_{z+\Delta z}} {\Delta z}$所以
$\frac{\partial \rho}{\partial t} = - \left ( \frac{\partial}{\partial x} (\rho u) + \frac{\partial}{\partial y} (\rho v) + \frac{\partial}{\partial z} (\rho w) \right ) = - \nabla \cdot \rho \textbf U$对控制体积分,运用高斯定理,可得连续性方程的积分形式
$\frac{\partial}{\partial t} \int \rho dV = - \oint \rho \textbf U \cdot \textbf n dS$ -
@simthere 你的问题其实可以简化为:为什么 $\int \rho dV = \rho_P \int dV$。(其中 $\rho_P$ 为格心处的流体密度)
下面给出简略证明:
我们假设P为单元格心,$\textbf x_P$ 为P点坐标,那么有如下定义
$\int (\textbf x - \textbf x_P) dV = 0$于是密度对控制单元的积分为:
$\int \rho dV = \int [\rho_P + (\textbf x - \textbf x_P) \cdot (\nabla \rho_P)] dV = \rho_P \int dV + (\nabla \rho_P) \cdot \int (\textbf x - \textbf x_P) dV = \rho_P \int dV$同理可以推广到压力、速度等物理量。


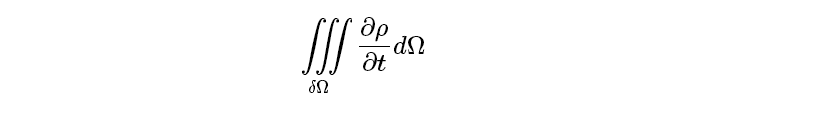


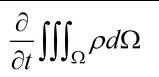 。
。