LES定义入口速度的问题（DSRFG方法）

[李东岳]

@霜染丹枫

完全的矩形，即三维槽道流

我不太清楚你们讨论的DSRFG这个东西。但是这种很难在三维槽道流内单纯凭这壁面保持湍流。你有没有试过添加扰动。

[霜染丹枫]

@李东岳 入口速度是在平均速度基础上加的扰动，这些扰动就是通过那个算法实现的，因此在每个时间步入口速度场的扰动时一直存在的。

[xjwang]

@李东岳 这个不仅仅是流槽了，算是风洞。虽然边界条件会有影响，但是不太影响计算域中的一些地方。

[xjwang]

@霜染丹枫 “根据自己的工况” 这句话，如果你的参数是从风洞试验中或者其他数据库中得到的，那应该没啥问题。不过我觉得，你貌似没有把紊流积分尺度等参数设置正确，一个比较快速的检查：你的网格尺寸是多少，你的紊流积分尺度是多少？看你发的那个图片，貌似是遇到了我之前那样的问题，脉动部分急剧减少。我现在手边没有我计算的图片，不过我的计算结果的瞬时速度场在整个计算域都能表现出明显的湍流特征。

[xjwang]

@李东岳 李老师，请问那个公众号下边回复说用CDRFG方法的同学或老师注册了吗？能否邀请他一起讨论一下那个方法？我一直感觉那篇论文中有一个错误，给作者发邮件也没回复。

[李东岳]

@xjwang 好像没有

[霜染丹枫]

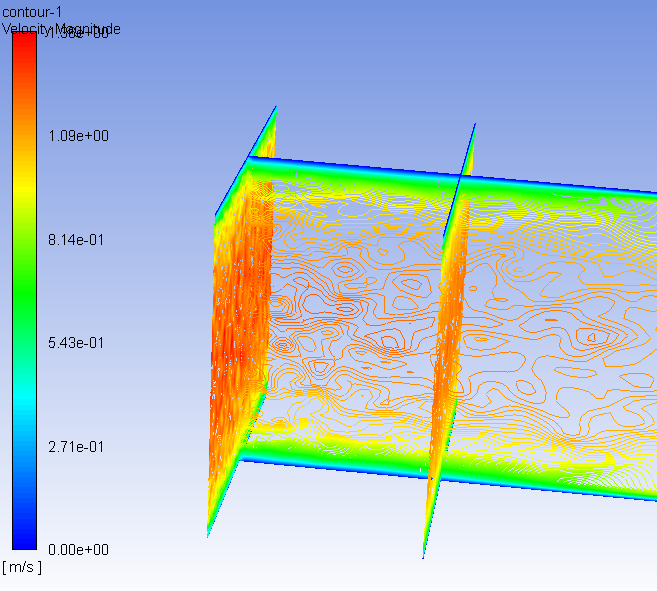
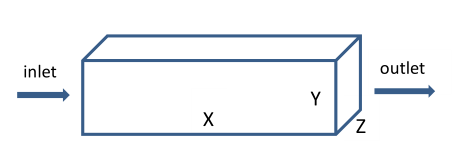
@xjwang 感谢回复，我的计算域如图所示，几何尺寸：X=1.2m、Y=0.2m、Z=0.4m。展向和轴向为均匀网格。空气沿x轴正向进入，平均速度是1.2m/s。入口采用速度入口边界条件，出口为压力出口边界条件，展向是周期性边界条件（即Z方向），上部和底部为壁面，采用无滑移边界条件。三个方向网格节点：64X64X128，垂直壁面方向采用非均匀网格，首层网格高度△y=0.0001m，保证Yplus<1。目前程序中湍流积分尺度设置为Ls=0.014（大致估算的，目前看来是有问题的）。Huang文章说这个参数很重要，给了三种设置的方法，但是我一直没引起重视。。。。您这个参数是如何来设置的呢？谢谢！

[李东岳]

后来他注册了，但是好像没来这里回复。

但是这种很难在三维槽道流内单纯凭这壁面保持湍流。你有没有试过添加扰动。

我是说初始internalField的扰动。

我看了一下Huang2010的文章，他们算的不是三维槽道流，里面包含障碍物，就不存在这个问题。但你那种三维槽道流很有可能有这个问题。

[霜染丹枫]

@李东岳 李老师，麻烦能说一下internalField的作用么，我不是很了解，谢谢

[xjwang]

@霜染丹枫 Ls太小吧，你这个算例感觉设置的不是太正确。
题外话：
1.你的首层网格高度0.0001m,不知道你具体咋划分的网格，沿高度方向如果增长太快的话，应该会对计算结果有影像，而且你网格的三个方向的尺寸比例如果出现这种1：1：1000这种情况的话，也会影响你的计算结果。
2.不知道你是不是想摸你ABL, 如果是的话，上部设置成无滑移边界条件不太好吧。

[xjwang]

@李东岳 internalField应该没啥影响，毕竟模拟时间比较长，初始条件可以忽略不计。我试过internalField是(0 0 0)和(U 0 0) 都没啥影响

[xjwang]

@霜染丹枫 还有你说的那三种Ls的计算方式很重要，但这个是影响空间相关性的。这个参数不是自己凭空造出的，我是根据试验来确定的

[李东岳]

@xjwang 在 定义入口速度的问题 中说：

internalField应该没啥影响，毕竟模拟时间比较长，初始条件可以忽略不计。我试过internalField是(0 0 0)和(U 0 0) 都没啥影响

有道理

[李东岳]

像是这种速度波动越往后越少的，类似开始有湍流后来无湍流，我倒是完全可以理解的。
持续关注解决办法

[xjwang]

@李东岳 对，这个可以理解，但是衰减太快就是有问题了，一般处理这种瞬态问题用的piso算法，会根据质量守恒去修正求解的速度，所以如果入口处不满足质量守恒，速度场会有很大的改变。

[霜染丹枫]

@xjwang 根据您的建议，我修改了湍流积分尺度，由于没有实验，这个量我是通过湍动能和耗散率来估算的。重新进行计算，目前能够看出下游流场表现出湍流状态。这个结果和您之前的计算发展趋势相似么，以说明我目前入口给定结果的正确性。

[霜染丹枫]

@李东岳 如李老师所言：“像是这种速度波动越往后越少的，类似开始有湍流后来无湍流”。我有个疑惑，采用中心差分格式的扩散项可以将扰动向四周传递，迎风格式的对流项具有迁移性，即可以将扰动向下游传递。从上面来看，入口的扰动应该是可以持续向下游传递的。如果几何轴向长度非常长的话，在很远的下游是不是也会保持一定湍流状态？还是由于壁面摩擦力及流体粘性对扰动有削减作用，在下游一直衰减甚至脉动全无，就是这种入口给定方法本身就会出现的现象呢？

[coolhhh]

这里是几点个人的看法：
1、DSRFG方法文章中，需要区分三维能量波谱与一维频谱的概念，下图DSRFG文章中公式(32)个人感觉是不能画等号的，因为表达的是不同维度的谱。DSRFG理论推导是生成满足三维能量谱的风场，CDRFG理论推导是生成满足一维频谱的风场。具体可搜索知网《基于傅里叶合成法的大气边界层脉动风场大涡模拟》(2018)文章中有相关阐述。

(引用：Huang S H, Li Q S, Wu J R. A general inflow turbulence generator for large eddy simulation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010,98(10-11):600-617.)

2、若采用von Karman频谱，von Karman频谱对频率的积分等于脉动动能，积分尺度Lu、Lv、Lw影响的是谱的峰值所对应的频率，对脉动动能的大小不产生影响。因此下面这个公式，利用了峰值频率的值来反推计算积分尺度。

(引用：庞加斌, 葛耀君, 陆烨. 大气边界层湍流积分尺度的分析方法[J]. 同济大学学报(自然科学版), 2002,30(5):622-626.)

3、入口处生成的是满足目标频谱的脉动风场，根据已经发表的文章计算结果(见下图)，LES总是会对入口处的脉动风过滤，最后的谱的形状在高频处总会衰减。根据频谱对频率的积分等于脉动动能，高频段被过滤，对应的脉动动能也会减小。

(引用：胡晓兵, 杨易. 基于NSRFG方法的标准地貌风场大涡模拟研究[J]. 工程力学, 2020,37(09):112-122.)

4、个人一直有个2疑问：
（1）入口处的风场严格满足了零散度要求，然后在LES是否就能无条件自保持？这个观点有无被证明了？
（2）积分尺度到底物理意义是什么？之前论文有个帖子有讨论过turbulence lenth scale 求助

感谢各位大佬指点迷津

[xjwang]

@coolhhh

1. 个人感觉是能画等号的，当f=kU. CDRFG方法中，对于定义p和q的时候，直接代入了Su,Sv,Sw, 而且还说有个系数halved，但后来检察代码发现没有减半。还有一个就是CDRFG方法是用来生成inhomogeneous inflow的，虽然从原始的RFG（Smirnov）中说，这个方式在生成inhomogeneous inflow的时候也可以近似看做零散度，但从CDRFG方法那个计算k,p,q的过程来看，应该能造成divergence.个人感觉这个方法之所以很多人用，也许是因为他们把程序贴在了文章后边。不过这也只是我个人感觉，如果我有错误的地方，还请指出来！！！
2. Lu,Lv,Lw虽然理论上来说不影响turbulence intensity，只是按你所说的那样，造成峰值的不同，但具体用到这个方法中，会有所影响。我们最近正完成了一篇论文讨论了这个情况，希望能快点见刊与大家分享。
3. 这个问题比较常见，虽然理论上来说，LES是对“大”涡进行解析模拟，而“小涡”进行SGS模拟，但还是会对高频处那些本应该解析模拟的部分不能精确模拟。
   4.严格说来，你看到的DSRFG方法并不是严格零散度，因为要考虑网格离散的影响。

[sunss]

你好同学，我最近再用NSRFG方法生成大气边界层风速入口，但不知道怎么将生成的风速数据导入openFoam中，看到你的这篇帖子后，尝试使用timeVaryingMappedFixedValue这个边界条件，但网上关于这个边界条件的用法几乎没有，而openFoam里有一个timeVaryingMappedFixedValue算例，但这个算例里U文件只有一步时间的数据，多步时间的格式不知道怎么写，请问你能告诉我U文件和point文件的格式吗，谢谢！我可以把我写的NSRFG方法分享出来，相互学习。