LES定义入口速度的问题(DSRFG方法)
-
各位老师专家好,我目前在做ABL的LES湍流入口时也碰到一些问题想和大家交流学习。我之前一直用Fluent来生成LES的湍流入口,近半年开始对Openfoam感兴趣,于是开始尝试把Fluent的相关算法移植到Openfoam当中,我采用的算法是华南理工杨易老师课题组提出的NSRFG算法,参考文献:
[1] Yu Y, Yang Y, Xie Z. A new inflow turbulence generator for large eddy simulation evaluation of wind effects on a standard high-rise building[J]. Building and Environment, 2018, 138: 300-313.
先把Fluent和of的计算结果图贴两张,我主要对PSD和湍流强度与平均风剖面进行了验证。
计算域
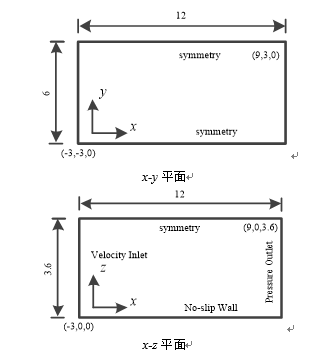
-
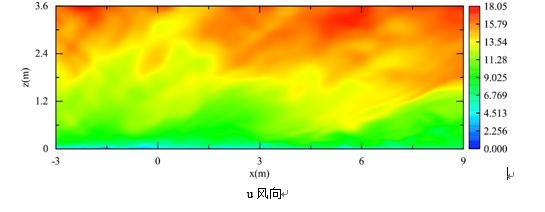
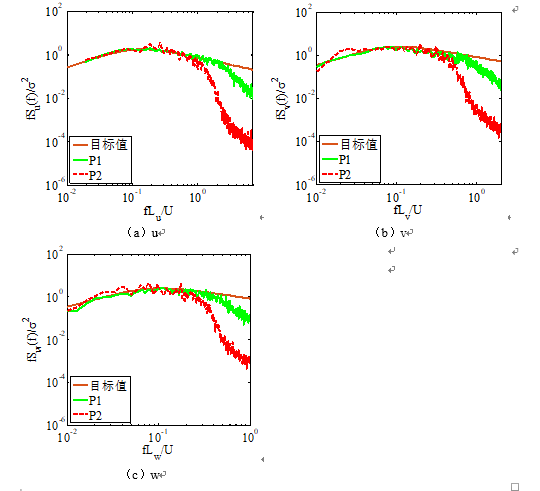
Fluent流场图及验证图
P1 是入口处的测点,P2是模型处的测点
-
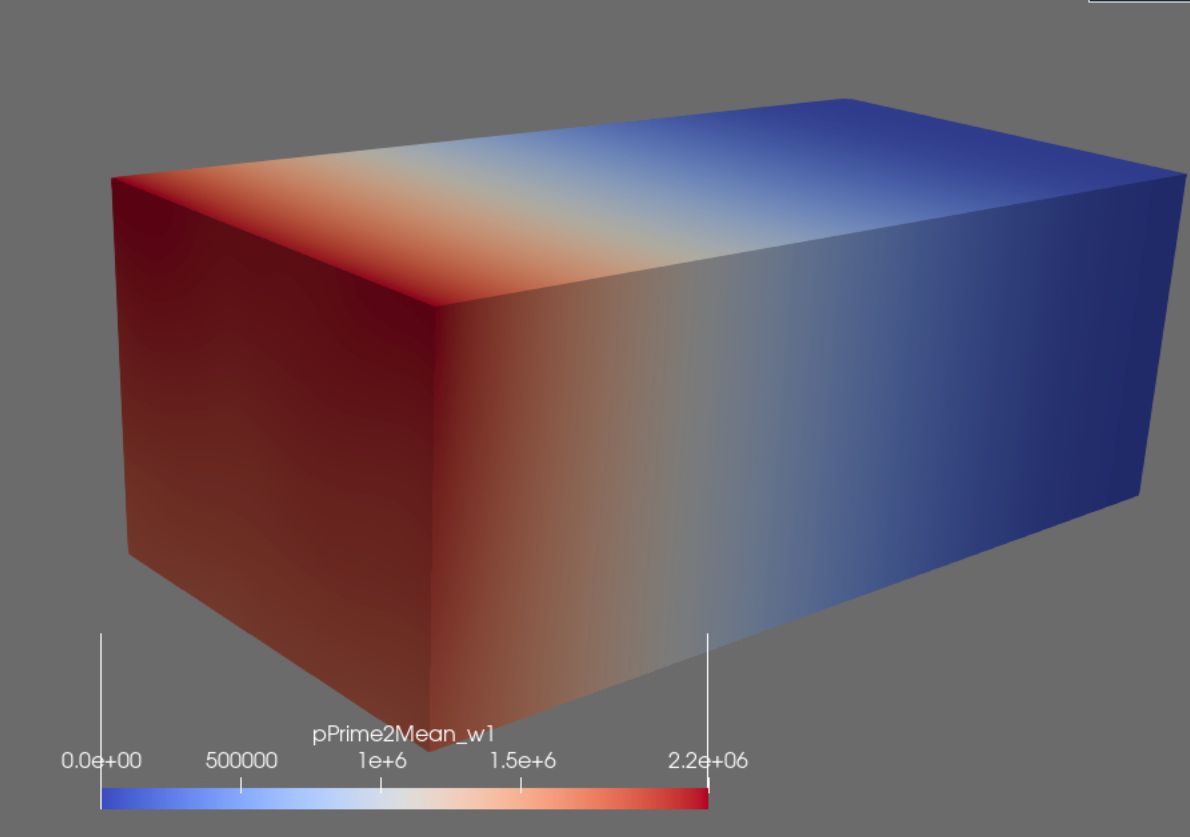
Openfoam流场图与验证图

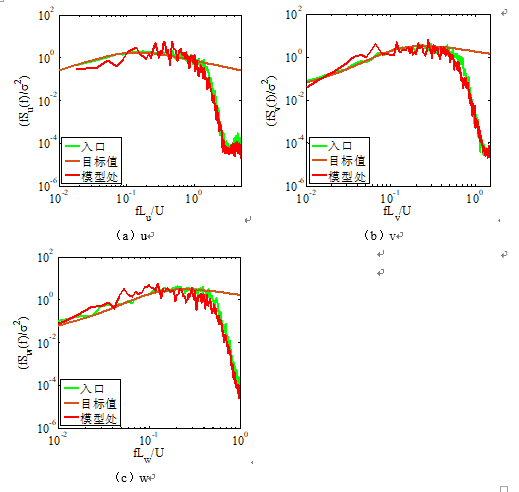
这里貌似of的结果还行,但实际上我认为Fluent的结果更合理,因为数值耗散等因素的影响,湍动能一定会在计算过程中耗散,因此模型处的PSD一定会更加吻合目标值。所以我目前怀疑我的case设置有问题,目前我采用的LES是WALE模型,0文件夹下应该要设置k 和 nut两个文件,我的设置分别如下:
/*--------------------------------*- C++ -*----------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Version: 6 \\/ M anipulation | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object k; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -2 0 0 0 0]; internalField uniform 0.0001; boundaryField { inlet { type fixedValue; value uniform 0; } ground { type kLowReWallFunction; //For high and low Re value $internalField; } top { type symmetry; } side1 { type symmetry; } side2 { type symmetry; } outlet { type zeroGradient; } } /*--------------------------------*- C++ -*----------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Version: 6 \\/ M anipulation | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object nut; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -1 0 0 0 0]; internalField uniform 1e-8; boundaryField { inlet { type zeroGradient; } ground { type nutUSpaldingWallFunction; value uniform 1e-8; } top { type symmetry; } side1 { type symmetry; } side2 { type symmetry; } outlet { type zeroGradient; } } // ************************************************************************* //这里我不太确定两个文件中internalField参数应该如何取值?另外,这两个参数对结果影响是否很大?请各位老师专家解答。谢谢!(P.S. of计算速度是真的快)
-
-
@xiaoyi0830 在 LES定义入口速度的问题(DSRFG方法) 中说:
@coolhhh 对于第一个问题,我也是晕了,三维能谱,一维能谱,功率谱怎么在这儿就混用了。
另外第四个问题,就算满足了连续性条件,也不会满足动量方程,所以进入计算域的速度肯定和入口处是有差别的。
-
@xiaoyi0830
1、功率谱计算。时间序列$ x(t) $计算时间相关函数$ R_{xx}(\tau) $,再进行傅里叶变换得到功率谱$ S_{xx}(\omega) $。
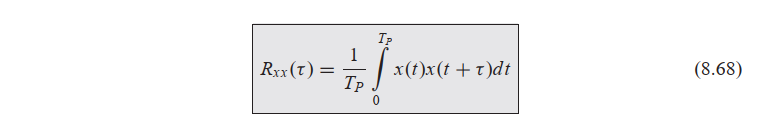
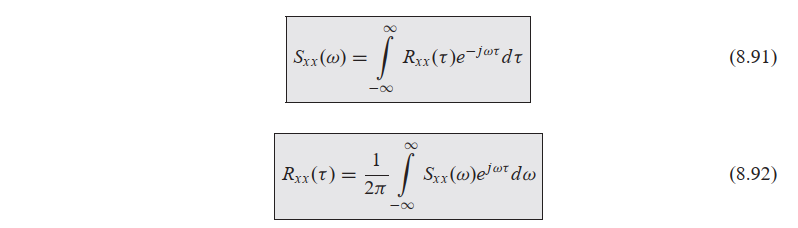
(引用:Shin K, Hammond J. Fundamentals of signal processing for sound and vibration engineers[M]. England: John Wiley & Sons, 2008:245.)2、风速功率谱。风速时程$ u(t) $对应时间序列$ x(t) $,求得的一维频谱(频域)就是对应此处的功率谱。一维频谱的自变量是频率或者角频率。
3、三维谱(波数域)。首先对三维空间相关函数进行三维的傅里叶变换得到的三维波谱,然后进行球面积分并乘以系数1/2,得到三维谱。因此要计算一个三维谱,需要整个三维空间的所有点的风速时程才能计算得到一个三维谱。


(引用:田内科斯 H., 兰姆利 J. L. 湍流初级教程[M]. 北京: 科学出版社, 2014:194-197.)4、一维波谱(波数域)。一维波谱是由一维空间相关函数(即一个空间方向的相关函数),进行一维的傅里叶变换得到的。与一维频谱类似,只是一个是频域,一个是波数域。
5、三维von Karman谱(均匀流场)表达式如下。针对于非均匀流场的三维von Karman谱表达式,个人未找到相关文章阐述。

(引用:Durbin P A, Pettersson Reif B A. Statistical theory and modeling for turbulent flows[M].Wiley, 2011:29-261.)6、三维von Karman谱与一维von Karman谱区别。
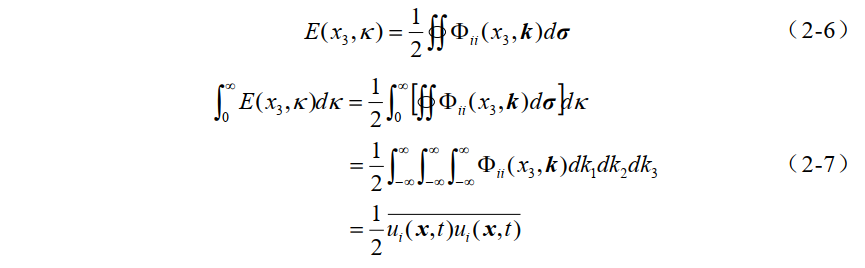
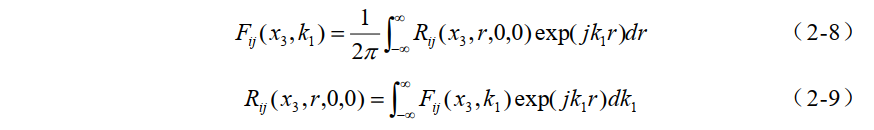

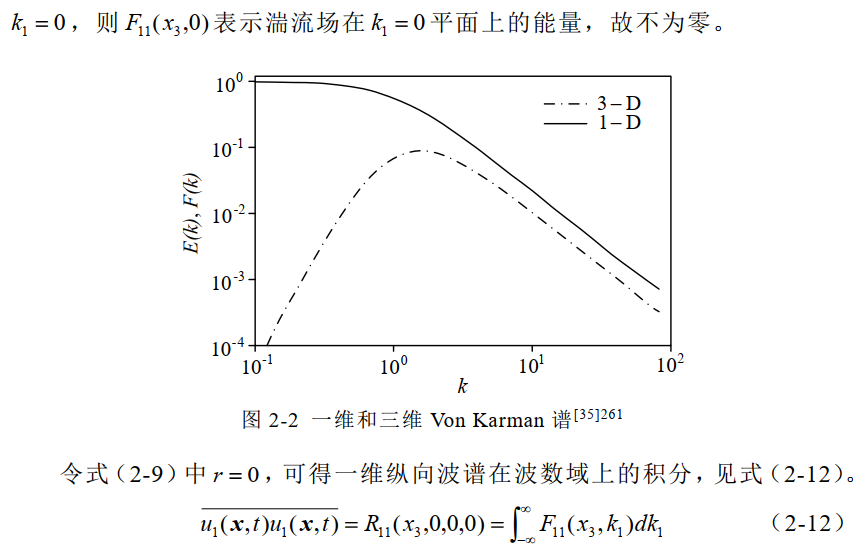

(引用:[1] Durbin P A, Pettersson Reif B A. Statistical theory and modeling for turbulent flows[M].Wiley, 2011:29-261.
[2] 陈铃伟. 基于傅里叶合成法的大气边界层脉动风场大涡模拟[D]. 黑龙江:哈尔滨工业大学,2017. DOI:10.7666/d.D01589559.)7、从《Diffusion by a Random Velocity Field》(Kraichan, 1970),到RFG方法,论文中都是未出现频谱的图,因为方法本身目标就是生成三维谱。DSRFG方法的理论推导也是实现三维谱,但是在应用方法时,用一维频谱表示三维谱,并最终的结果用频谱图表示,这与三维谱的原始定义是不同概念的,这两者不应该混淆。
8、CDRFG、NSRFG的理论推导就是为实现一维频谱。CDRFG方法既然目标实现频谱,可以简化一个循环,如下阐述
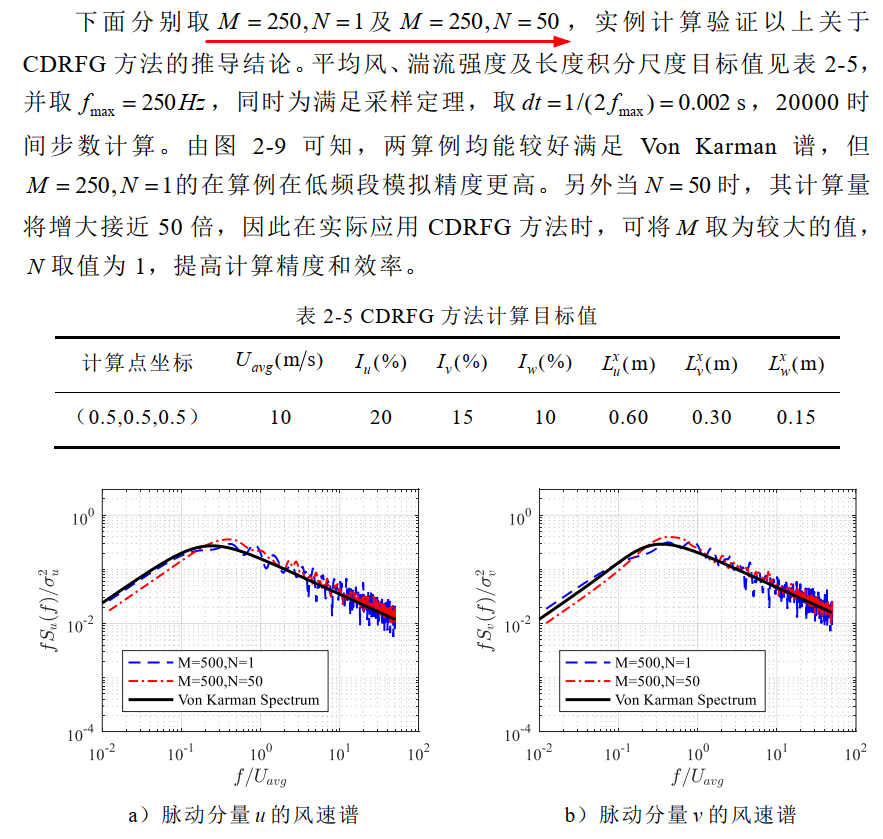
(引用:陈铃伟. 基于傅里叶合成法的大气边界层脉动风场大涡模拟[D]. 黑龙江:哈尔滨工业大学,2017. DOI:10.7666/d.D01589559.)9、CDRFG方法的P、Q的原论文的公式有误,在原作者后来发的一篇文章中已对其进行了更正。
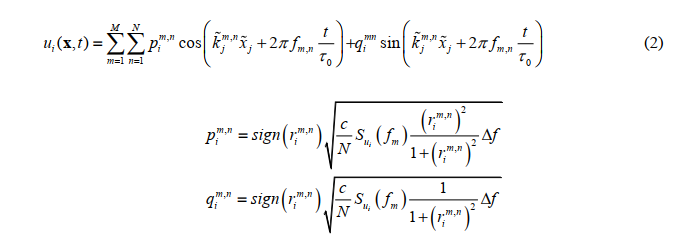
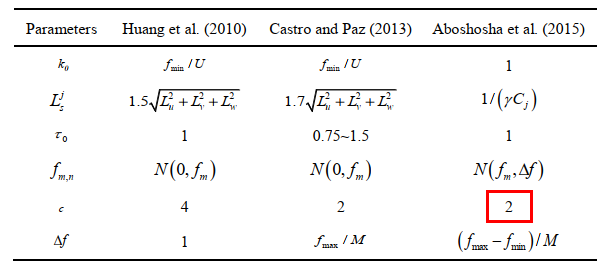
(引用:Melaku A, Bitsuamlak G, Elshaer A, et al. Synthetic inflow turbulence generation methods for LES study of tall building aerodynamics[J]. 2017.) -
NSRFG湍流入口合成方法分享(我在验证结果的时候发现NSRFG方法和CDRFG方法均存在水平方向流场均一性问题,不知道对不对)。
%% NSRFG湍流合成方法 tic clc,clear %%生成0-fmax Hz范围的功率谱 fmax=25;df=0.001;fw=df:df:fmax; N=length(fw); fm=(2*(1:N)-1)/2*df; Time_NSRFG=1000;%时间点数量 h=1/fmax/2;%时间步长 Fs=1/h; %%入口尺寸和模拟点数量设置 x=1;%流场方向坐标 y=1;%水平方向坐标 z=[linspace(0.01,0.1,10),linspace(0.11,0.5,20),linspace(0.55,1,10)];%竖直方向坐标 N0_Y=length(y);N0_Z=length(z);N0_X=length(x);%X,Y,Z对应u,v,w,各方向上的点数 xyz=[repmat(x,length(z)*length(y),1),... repmat(y',length(z),1),... reshape(repmat(z,length(y),1),[],1)]'; %%切分Time_NSRFG成N0_T段,避免内存溢出 memory_capacity=0.4*10^9;%16G内存建议取值,内存越大计算速度越快 N0_t=min(fix(memory_capacity/(N0_Z*N0_Y)/N),Time_NSRFG); N0_T=ceil(Time_NSRFG/N0_t); %%相关性参数设置, c_1=10;c_2=12;c_3=12; Gammaix=1.8;Gammaiy=1.5;Gammaiz=1.8; %%风场特性-风速 z_ref=0.4;%标准参考高度 alpha=0.25;%粗糙度指数 U_ref=10.0;%参考风速 I_10=0.23; coefv=0.88; coefw=0.55; Uav=U_ref*(z/z_ref).^alpha; Uav_map=(reshape(repmat(Uav,N0_Y,1),[],1))'; %%风场特性-湍流强度 Iu=0.1*(z/z_ref).^(-alpha-0.05); Iv=coefv*Iu; Iw=coefw*Iu; I_map=[(reshape(repmat(Iu,N0_Y,1),[],1)),... (reshape(repmat(Iv,N0_Y,1),[],1)),... (reshape(repmat(Iw,N0_Y,1),[],1))]';= %%风场特性-积分尺度 z_0=0.25; Lu=linspace(0.25,1,N0_Z); Lv=0.5*coefv^3*Lu; Lw=0.5*coefw^3*Lu; L_map=[(reshape(repmat(Lu,N0_Y,1),[],1)),... (reshape(repmat(Lv,N0_Y,1),[],1)),... (reshape(repmat(Lw,N0_Y,1),[],1))]'; %初始化参数 Su=zeros(N,N0_Z*N0_Y);Sv=zeros(N,N0_Z*N0_Y);Sw=zeros(N,N0_Z*N0_Y); p_uvw=zeros(3,N); p_u=zeros(N,N0_Z*N0_Y);p_v=zeros(N,N0_Z*N0_Y);p_w=zeros(N,N0_Z*N0_Y); Lx=zeros(N,N0_Z*N0_Y);Ly=zeros(N,N0_Z*N0_Y);Lz=zeros(N,N0_Z*N0_Y); q_1n=zeros(N,N0_Z*N0_Y);q_2n=zeros(N,N0_Z*N0_Y);q_3n=zeros(N,N0_Z*N0_Y); A_n=zeros(N,N0_Z*N0_Y);B_n=zeros(N,N0_Z*N0_Y); k_1n=zeros(N,N0_Z*N0_Y);k_2n=zeros(N,N0_Z*N0_Y);k_3n=zeros(N,N0_Z*N0_Y); K_xyz=zeros(3,N0_Z*N0_Y,N); x_1n=zeros(N,N0_Z*N0_Y);x_2n=zeros(N,N0_Z*N0_Y);x_3n=zeros(N,N0_Z*N0_Y); X_xyz=zeros(3,N0_Z*N0_Y,N); U_u0=zeros(N0_t,N0_Z*N0_Y,N);U_v0=zeros(N0_t,N0_Z*N0_Y,N);U_w0=zeros(N0_t,N0_Z*N0_Y,N); U_u=zeros(1,N0_Z*N0_Y);U_v=zeros(1,N0_Z*N0_Y);U_w=zeros(1,N0_Z*N0_Y); %球面随机采样 S = randn(N,3); sign_n =bsxfun(@rdivide, S, sqrt(sum(S.*S, 2))); plot3(sign_n(:,1),sign_n(:,2),sign_n(:,3),'.k', 'MarkerSize',10) %绘制原始散点数据 %%生成随机数\thea_n thea_n=2*pi*rand(N+100,N0_Z*N0_Y); fm=(2*(1:N)-1)/2*df; %%生成参数矩阵 parfor n=1:N%频率范围 disp('n');disp(n); Su(n,:)=4*(I_map(1,:).*Uav_map).^2.*(L_map(1,:)./Uav_map)./... (1+70.8*(fm(n)*L_map(1,:)./Uav_map).^2).^(5/6);%Karman Sv(n,:)=4*(I_map(2,:).*Uav_map).^2.*(L_map(2,:)./Uav_map).*... (1+755.2*(fm(n)*L_map(2,:)./Uav_map).^2)./((1+283.2*(fm(n).*L_map(2,:)./Uav_map).^2).^(11/6));%Karman Sw(n,:)=4*(I_map(3,:).*Uav_map).^2.*(L_map(3,:)./Uav_map).*... (1+755.2*(fm(n)*L_map(3,:)./Uav_map).^2)./((1+283.2*(fm(n).*L_map(3,:)./Uav_map).^2).^(11/6));%Karman p_u(n,:)=sign(sign_n(n,1))*sqrt(2*Su(n,:)*df); p_v(n,:)=sign(sign_n(n,2))*sqrt(2*Sv(n,:)*df); p_w(n,:)=sign(sign_n(n,3))*sqrt(2*Sw(n,:)*df); Lx(n,:)=U_ref./((fm(n)))./c_1./Gammaix; Ly(n,:)=U_ref./((fm(n)))./c_2./Gammaiy; Lz(n,:)=U_ref./((fm(n)))./c_3./Gammaiz; q_1n(n,:)=p_u(n,:)./Lx(n,:); q_2n(n,:)=p_v(n,:)./Ly(n,:); q_3n(n,:)=p_w(n,:)./Lz(n,:); A_n(n,:)=sqrt((q_2n(n,:).^2+q_3n(n,:).^2).^2+(q_1n(n,:).*q_2n(n,:)).^2+(q_1n(n,:).*q_3n(n,:)).^2); B_n(n,:)=sqrt(q_2n(n,:).^2+q_3n(n,:).^2); k_1n(n,:)=-(q_2n(n,:).^2+q_3n(n,:).^2)./A_n(n,:).*sin(thea_n(n,1)); k_2n(n,:)=(q_1n(n,:).*q_2n(n,:))./A_n(n,:).*sin(thea_n(n,1))+q_3n(n,:)./B_n(n,:).*cos(thea_n(n,1)); k_3n(n,:)=(q_1n(n,:).*q_3n(n,:))./A_n(n,:).*sin(thea_n(n,1))-q_2n(n,:)./B_n(n,:).*cos(thea_n(n,1)); div1(n,:)=q_1n(n,:).* k_1n(n,:)+q_2n(n,:).* k_2n(n,:)+q_3n(n,:).* k_3n(n,:); div2(n,:)= k_1n(n,:).* k_1n(n,:)+ k_2n(n,:).* k_2n(n,:)+ k_3n(n,:).* k_3n(n,:); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% K_xyz(:,:,n)=[k_1n(n,:);k_2n(n,:);k_3n(n,:)];%3x9 x_1n(n,:)=(xyz(1,:))./Lx(n,:); x_2n(n,:)=(xyz(2,:))./Ly(n,:); x_3n(n,:)=(xyz(3,:))./Lz(n,:); X_xyz(:,:,n)=[x_1n(n,:);x_2n(n,:);x_3n(n,:)];%3x9 kjxj(n,:)=(diag(K_xyz(:,:,n)'*X_xyz(:,:,n)))'; end;disp('完成构建矩阵'); %%合成风速 leq_n=2*pi*rand(3,N); t=(1:1:N0_t)*h; ru=sign_n(:,1);rv=sign_n(:,2);rw=sign_n(:,3); for it=1:N0_T for n=1:N disp(['N0_T--','it--','n','运行时间: ',num2str([N0_T,it,n,toc])]); U_u0(:,:,n)=p_u(n,:).*sin(repmat(kjxj(n,:),N0_t,1)+2*pi*fm(n).*t'+repmat(leq_n(1,n),N0_t,1)); U_v0(:,:,n)=p_v(n,:).*sin(repmat(kjxj(n,:),N0_t,1)+2*pi*fm(n).*t'+repmat(leq_n(1,n),N0_t,1)); U_w0(:,:,n)=p_w(n,:).*sin(repmat(kjxj(n,:),N0_t,1)+2*pi*fm(n).*t'+repmat(leq_n(1,n),N0_t,1)); end;t=t+N0_t*h; U_u=cat(1,U_u,sum(U_u0,3)); U_v=cat(1,U_v,sum(U_v0,3)); U_w=cat(1,U_w,sum(U_w0,3)); end U=roundn(U_u(2:end,:)+Uav_map,-4)'; V=roundn(U_v(2:end,:),-4)'; W=roundn(U_w(2:end,:),-4)'; toc disp(['运行时间: ',num2str(toc)]); disp('=====accomplish======') -
@xjwang 在 LES定义入口速度的问题(DSRFG方法) 中说:
@sunss
应该是在constant/boundaryData/inlet文件夹下边有一个points的文件,然后每一个时间步都是一个文件夹,其中包含一个U文件。比如说,我在inlet文件夹下边在terminal中输入ls,会显示:0 0.001 0.002 ...... points
而在每一个时间步文件夹下输入ls,比如在0.001文件夹下,会显示:
U
您好,我想请教一下这个数据的事情。在foam中运用并行运算,是在分块前面把inlet坐标输出然后运用算法求出inlet上每个点对应的风速,然后按照您的方法导入到constant/boundaryData/inlet中吗?还是在分块后,按照该方法进行呢?
-
@BznW 压力脉动问题主要是因为入口质量通量不平衡导致的,NSRFG原论文中算出来的脉动压力系数也是非常大。简单的入口质量通量修正可以参考以下文章:
1.《Kim, Y., I.P. Castro and Z. Xie, Divergence-free turbulence inflow conditions for large-eddy simulations with incompressible flow solvers. Computers & Fluids, 2013. 84: p. 56-68.》
2.《Wang, Y. and X. Chen, Simulation of approaching boundary layer flow and wind loads on high-rise buildings by wall-modeled LES. Journal of Wind Engineering and Industrial Aerodynamics, 2020. 207: p. 104410.》