fluent用LES算水翼边界层选择中心差分引起的震荡如何消除
-
各位大佬好,小弟最近在用fluent算一个扭曲水翼的边界层速度剖面(约1~4mm以下的区域),雷诺数在5e5的量级。经过个把月的计算尝试,排除各种影响因素,现在确定只有中心差分能把边界层速度剖面和脉动量与LDV实验对上,其他差分格式包括有界中心差分(bounded central difference)都带有迎风性质,老师说迎风数值粘性大,可能因此在近壁区域与实验相差较大。
但问题如图,中心差分会在瞬时速度流场存在轻微的震荡,导致涡量表示会有一些碎涡,并且速度场等值面也会不光滑,不知道如何消除,看有的文献貌似是加一个滤波将震荡消除,但是不是很清楚具体做法,不知道各位大佬有何高招。
已经排除的因素如下:
1.网格 数量1000w左右,展向流向法向都经过反复调整,震荡不会因为网格的变化而改变,确定不是网格的问题,并且尝试了非结构的八叉树网格,这样除了边界层几乎是各项同性,仍然会有震荡。
2.LES模型,主要采用的WALE,湍流常数0.325,0.5没有明显区别
3.边界条件,全流道或半个水翼,无影响,进出口速度压力不同组合也无影响
4.速度压力耦合或解耦simple simplec,无影响
5.进口或出口长度, 进口4倍弦长,出口5倍弦长,应该足够了
6.时间步长 从5e-6到5e-5,确定跟CFL数无关,所有库朗数都小于1也会震荡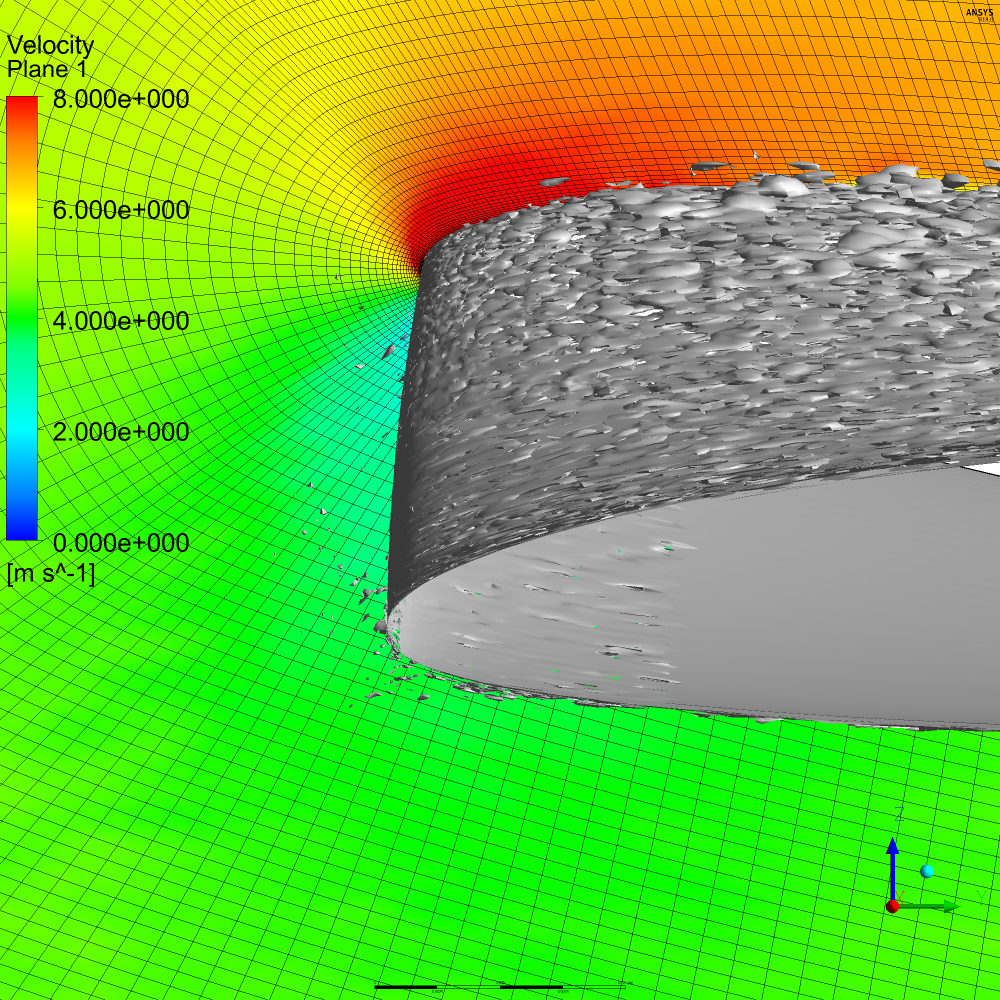
-
感谢李老师的及时回复!目前情况是这样
- https://aip.scitation.org/doi/pdf/10.1063/1.5045795 文献引用的文献[23]提到了一种filter,但是并不清楚怎样应用到fluent
- 试过dynamic也会震荡,貌似跟模型无关,因为要算边界层还是主要用WALE
3.目前fluent自带的差分格式包括upwind, 2nd upwind, 3ord MUSCL, quick, bound cd 和cd都试了,只有cd能比较精确的算准边界层的速度剖面和脉动强度,检索到涉及定量分析边界层的文献比如槽道流动,平板流动,绝大多数也是用的中心差分,只是雷诺数都偏低。
震荡并不影响边界层平均速度和脉动与实验的对照,但是瞬时流场会有这样的锯齿形状,所以Q涡显示时会有一些非物理的碎涡出现,怎么都感觉会对后处理有影响。。

-
感谢老铁的建议,我查了查好像没有这种现成的耦合操作,bounded cd可能是最像的,但是经过计算发现在边界层应该是全部切换成迎风格式了,没有部分耦合这种机制。

在国外cfd论坛上找到一个相似的情况,幸运的是那个人好像不关注边界层就改成迎风就没有震荡了,我看有个人的回答也解释了为什么除了中心差分都算不太准边界层。。
The choice of the scheme for LES should be based on the numerical diffusion it introduces. Ideally you should use linear(中心差分), or cubic. You need good and prett uniform mesh anyways for LES, since you are assuming the filter operator and the differential operator are commutative, which is not true on non-uniform grids! The filtered schemes are a last resort scheme in my view, if you can't really do better with your mesh. Upwind and linearUpwind, but also limitedLinear and QUICK should be avoided because they are too dissipative.
可惜就是无法消除震荡
-
李老师,可以先看下0.15弦长处的速度剖面,我是在这个位置插入一根沿z方向4mm线导出平均速度,x=0.0002m, y=-0.059182m, z=0.016964m到0.020964m,根据最大值无量纲化,图表附在文件里。velocity_profile_ldv_test_0.15C.zip
-
抱歉,李老师,那我直接把LDV的数据贴上吧,谢谢老师!
0.51874 0.02 0.54523 0.04 0.57821 0.06 0.60027 0.08 0.61619 0.1 0.63168 0.12 0.65259 0.16 0.67519 0.2 0.69035 0.24 0.71312 0.28 0.72578 0.32 0.75144 0.38 0.76757 0.42 0.78385 0.46 0.79825 0.5 0.81624 0.54 0.83174 0.58 0.86305 0.66 0.89698 0.74 0.9205 0.82 0.94188 0.9 0.96355 0.98 0.98842 1.14 0.99863 1.3 1.00000 1.46 0.99797 1.62 0.99706 1.78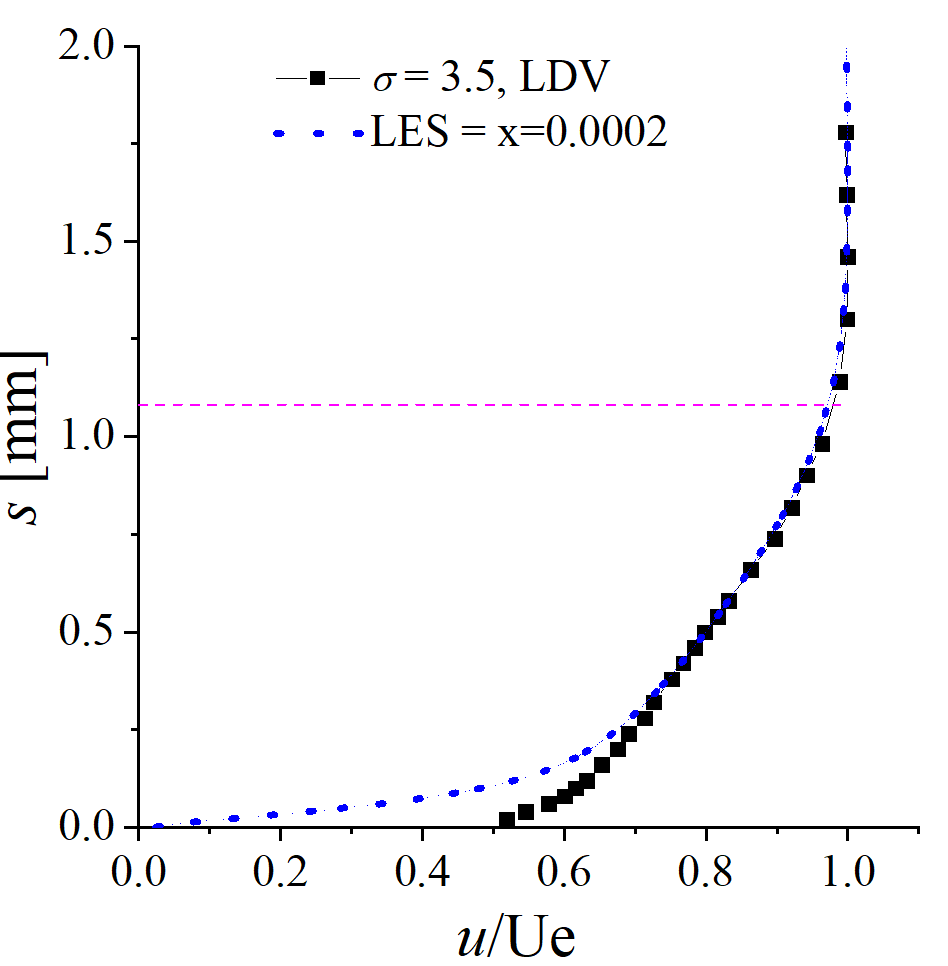
-
- is it time-averaged U predicted by LES?
- What is the maxima? the Umax in this line or in the computational domain?
Your results look quite good. Is it predicted by linear scheme? How about the other schemes, e.g., limited schemes?
I am runing LES simulation, but it is very slow. I try to limit Co under 0.6. Since the global Umax is around 10 m/s, it indicates $\Delta t = 2.6e-6$. What value is your global Umax?
Courant Number mean: 0.00518159 max: 0.59921 deltaT = 2.67779e-06 Time = 0.0168822 GAMG: Solving for p, Initial residual = 0.0474207, Final residual = 0.00156874, No Iterations 2 time step continuity errors : sum local = 3.90116e-10, global = -6.12223e-14, cumulative = 5.73243e-11 DICPCG: Solving for p, Initial residual = 0.0105353, Final residual = 9.99036e-07, No Iterations 608 time step continuity errors : sum local = 2.48515e-13, global = -3.59741e-15, cumulative = 5.73207e-11 ExecutionTime = 401.48 s ClockTime = 421 s fieldMinMax minMaxp write: min/max(mag(U)) = 0 10.5464 Courant Number mean: 0.0051816 max: 0.601813 deltaT = 2.61829e-06 Time = 0.0168848 GAMG: Solving for p, Initial residual = 0.0479045, Final residual = 0.00156265, No Iterations 2 time step continuity errors : sum local = 3.72593e-10, global = 2.37179e-14, cumulative = 5.73444e-11 DICPCG: Solving for p, Initial residual = 0.0102726, Final residual = 9.97099e-07, No Iterations 152 time step continuity errors : sum local = 2.38352e-13, global = 2.12724e-14, cumulative = 5.73657e-11 ExecutionTime = 402.54 s ClockTime = 423 s





 您有时间的话可以试试foam的中心差分格式,我用CFX和fluent都会有震荡。这是约450万的网格文件:
您有时间的话可以试试foam的中心差分格式,我用CFX和fluent都会有震荡。这是约450万的网格文件: