LES直流槽道边界层模拟,如何得到正则化速度u+以及正则化坐标y+?
-
各位老师同学好,我正在用大涡模拟做一个直流槽道边界层模拟,雷诺数
$${\rm Re} _{\tau } = u _\tau h / \nu = 1000$$
其中$h$为槽道半高,$ u _\tau$为摩擦速度,$\nu$为运动粘度。根据Pope在Turbulent Flows一书中提到的公式
$${{\mathop {\rm Re} \nolimits} _\tau } \approx 0.09 {{\mathop {\rm Re} \nolimits} ^ {0.88}}$$
估计槽道的雷诺数为
$${\mathop{\rm Re}\nolimits} = {U_m}\left( {2h} \right)/\nu =3.9578e4\approx4e4$$
其中${U_m}$为平均流速。
所以我将OpenFOAM自带的槽道流算例channel395拿来,对于它的半高$h=1m$,运动粘度$\nu=2e-5m^2/s$的槽道,${U_m=0.4m/s}$。我修改了一下平均速度和网格。
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object fvOptions; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // momentumSource { type meanVelocityForce; selectionMode all; fields (U); Ubar (0.4 0 0); } // ************************************************************************* //网格划分,粘性长度$\delta_\nu=h/{Re_{\tau}}=1e-3$。LES的网格尺寸建议为
$$50 \le \Delta {x^ + } \le 150,\Delta y_{wall}^ + < 1,15 \le \Delta {z^ + } \le 40$$
我使用的网格$\Delta {x^ + } =100$,$\Delta {z^ + } =50$,$\Delta {z^ + }$超了点,不过影响应该不会太大。
关键在于$\Delta {y}$,在于槽道半高范围内60个网格,最后一个网格的长度是第一个网格长度的25倍,算下来第一个网格的尺寸0.001103718,就是1个粘性长度多一点。
网格是符合要求的。FoamFile { version 2.0; format ascii; class dictionary; object blockMeshDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // scale 1; vertices ( (0 0 0) (4 0 0) (0 1 0) (4 1 0) (0 2 0) (4 2 0) (0 0 2) (4 0 2) (0 1 2) (4 1 2) (0 2 2) (4 2 2) ); blocks ( hex (0 1 3 2 6 7 9 8) (40 60 30) simpleGrading (1 25 1) hex (2 3 5 4 8 9 11 10) (40 60 30) simpleGrading (1 -25 1) ); edges ( ); boundary ( bottomWall { type wall; faces ((0 1 7 6)); } topWall { type wall; faces ((4 10 11 5)); } sides1_half0 { type cyclic; neighbourPatch sides1_half1; faces ((0 2 3 1)); } sides1_half1 { type cyclic; neighbourPatch sides1_half0; faces ((6 7 9 8)); } sides2_half0 { type cyclic; neighbourPatch sides2_half1; faces ((2 4 5 3)); } sides2_half1 { type cyclic; neighbourPatch sides2_half0; faces ((8 9 11 10)); } inout1_half0 { type cyclic; neighbourPatch inout1_half1; faces ((1 3 9 7)); } inout1_half1 { type cyclic; neighbourPatch inout1_half0; faces ((0 6 8 2)); } inout2_half0 { type cyclic; neighbourPatch inout2_half1; faces ((3 5 11 9)); } inout2_half1 { type cyclic; neighbourPatch inout2_half0; faces ((2 8 10 4)); } ); mergePatchPairs ( ); // ************************************************************************* //接下来是边界条件。
边界条件k,后面都是周期边界的cyclicFoamFile { version 2.0; format ascii; class volScalarField; location "1"; object k; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { bottomWall { type fixedValue; value uniform 0; } topWall { type fixedValue; value uniform 0; }边界条件nut
FoamFile { version 2.0; format ascii; class volScalarField; location "1"; object nut; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -1 0 0 0 0]; internalField uniform 0; boundaryField { bottomWall { type zeroGradient; } topWall { type zeroGradient; }边界条件nuTuilda
FoamFile { version 2.0; format ascii; class volScalarField; location "1"; object nuTilda; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -1 0 0 0 0]; internalField uniform 0; boundaryField { bottomWall { type fixedValue; value uniform 0; } topWall { type fixedValue; value uniform 0; }边界条件p
FoamFile { version 2.0; format ascii; class volScalarField; location "1"; object p; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { bottomWall { type zeroGradient; } topWall { type zeroGradient; }边界条件U
FoamFile { version 2.0; format ascii; class volVectorField; location "1"; object U; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 1 -1 0 0 0 0]; internalField uniform (0.4 0 0); boundaryField { bottomWall { type noSlip; } topWall { type noSlip; }
算了很长时间,可以保证是完全发展了。channel395也就算到了1000s,后来我还往后延长算了一些,1000s是足够的。我这个channel1000算500000s肯定够了。
controlDictFoamFile { version 2.0; format ascii; class dictionary; location "system"; object controlDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // application pimpleFoam; startFrom latestTime; startTime 0; stopAt endTime; endTime 500000; deltaT 0.1; writeControl timeStep; writeInterval 100000; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable true; functions { #includeFunc yPlus #includeFunc wallShearStress fieldAverage1 { type fieldAverage; libs (fieldFunctionObjects); writeControl writeTime; fields ( U { mean on; prime2Mean on; base time; } p { mean on; prime2Mean on; base time; } ); } }算出来的结果使用postChannel工具进行空间平均,得到平均速度随y坐标变化的两组数,储存在 graphs/时间文件/Uf.xy 中。
例如130000s的时候0.00110372 0.0133657 0.00337304 0.0407483 0.00576962 0.0693065 0.00830057 0.0985189 0.0109734 0.127533 0.0137962 0.155335 0.0167772 0.181026 0.0199254 0.204059 0.0232501 0.224291 0.0267613 0.241887 0.0304693 0.257159 0.0343852 0.270453 0.0385207 0.282087 0.0428881 0.292333 0.0475004 0.301416 0.0523713 0.309517 0.0575154 0.316783 0.0629479 0.323336 0.068685 0.329275 0.0747438 0.334681 0.0811423 0.339623 0.0878997 0.34416 0.0950359 0.348342 0.102572 0.352215 0.110531 0.355819 0.118936 0.359191 0.127813 0.362361 0.137187 0.36536 0.147087 0.368214 0.157542 0.370948 0.168584 0.373584 0.180244 0.376144 0.192558 0.378647 0.205563 0.381111 0.219297 0.383551 0.233801 0.385977 0.249118 0.3884 0.265294 0.390826 0.282378 0.393261 0.300419 0.395709 0.319472 0.398174 0.339593 0.400655 0.360842 0.403151 0.383283 0.40566 0.406982 0.40818 0.43201 0.410709 0.458442 0.413247 0.486356 0.415792 0.515834 0.41834 0.546966 0.420883 0.579844 0.423407 0.614565 0.425894 0.651232 0.428324 0.689956 0.43067 0.730852 0.432905 0.77404 0.434979 0.81965 0.436819 0.867818 0.43835 0.918686 0.439484 0.972407 0.4401
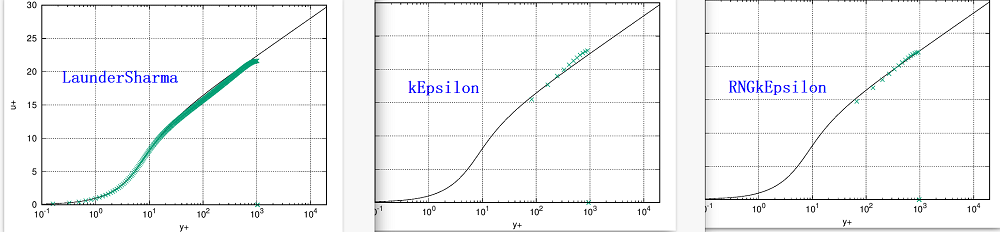
接下来就是正则化,画出速度分布了。别人的$ {\rm Re} _ {\tau } = 177.6 $结果是这样的。
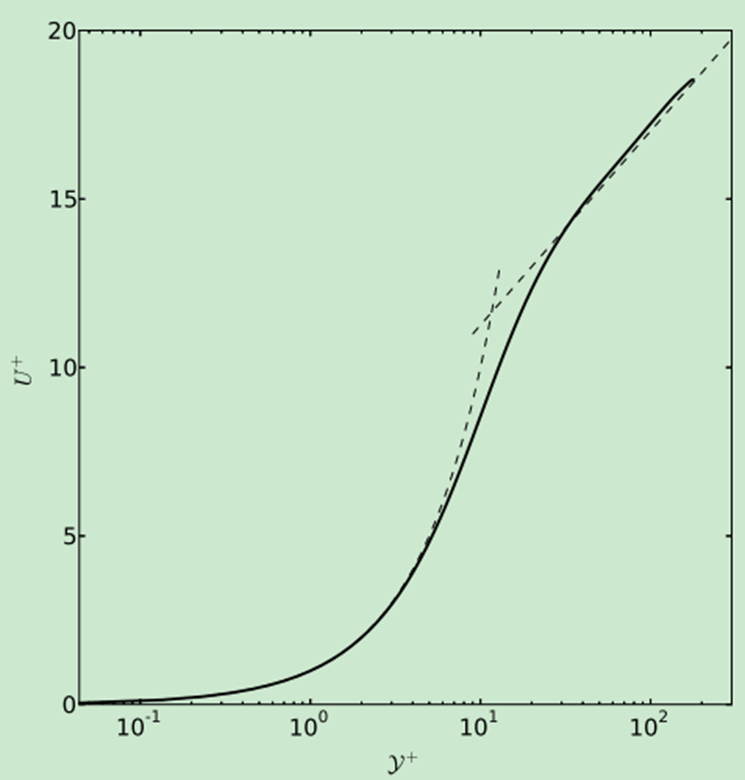
正则化的关键在于计算摩擦速度$ u_{\tau} $,$ u^{+}=u/u_{\tau} $,$ y^{+}=yu_{\tau} / \nu $。
我这边使用了两种计算摩擦速度的方法。
第一种是认为此算例的摩擦雷诺数就是标称的1000,因此直接利用公式$u_{\tau }={\rm Re}_{\tau }\nu/h$计算摩擦速度。可以看到在50000s后,速度曲线在对数率部分与理论解吻合上了。但所有时间的速度曲线在粘性底层都无法和线性率的理论解对应。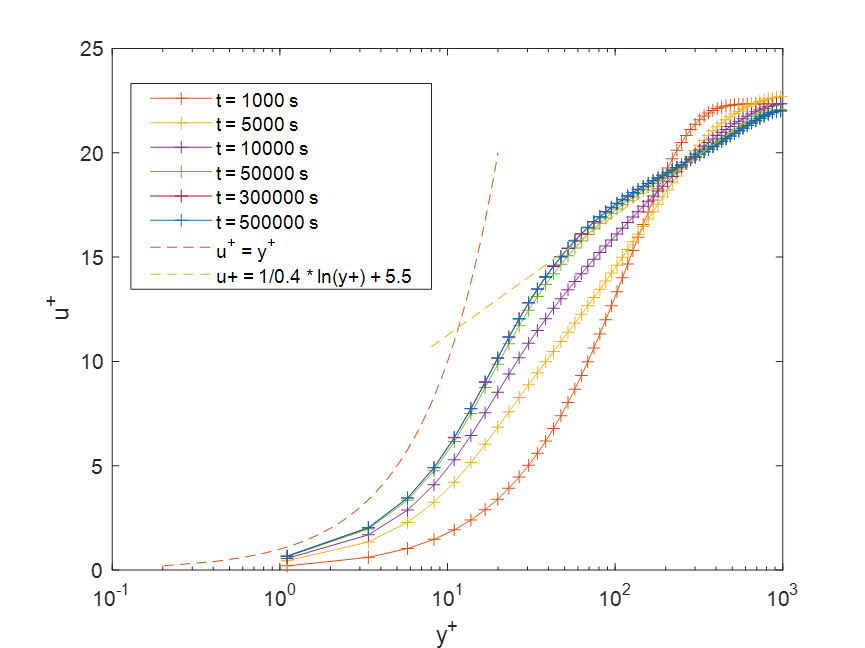
第二种方法是,通过计算出来的速度-高度曲线,实际地进行计算,${u_\tau } = \sqrt {\nu {{\left. {\frac{{du}}{{dy}}} \right|}_{y = 0}}} $。这种方法画出的速度曲线在粘性底层(也就是线性率部分)和理论解是对应得上的。但是在对数率部分,数值结果明显过高,但可以看到50000s及之后的数值结果曲线和理论解的线基本平行的,就好像是理论解应该再高一些,数值结果就和理论解完美吻合了。
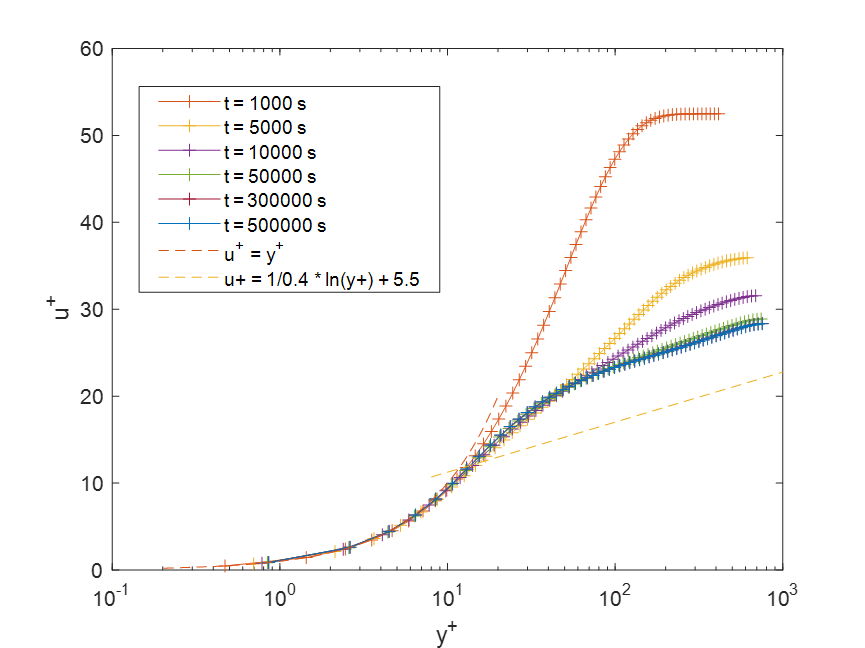
已经卡在这个问题上好久了。
应该不是网格的问题,现在的网格是符合要求的。
不是湍流没发展出来的问题,因为channel395计算的结果,我画出来也和上面这两张图差不多,所以感觉还是正则化的问题。
但感觉又不是正则化的问题,因为最终决定的因素就是摩擦速度,我也尝试过给一个具体的摩擦速度值,看看数值结果的曲线的形状能不能和理论解对得上,结果就像第一种方法画出来的图,对数率部分吻合了,粘性底层就差太多了。
看别人的图真真好看,比如那张绿底的。
求各位大佬指点迷津,我哪里做的不对?
也欢迎各位同学一起讨论,互相指点,少走弯路。
PS1:不知道上面的代码发出来会不会折叠,发帖预览的时候没有折叠感觉好长,有点担心实际效果。
PS2:插入在段落中的代码有时候不会被转写,至少是在预览界面。 -
排版非常好。
你用的是层流模拟么,还是什么湍流模型?没看到你用什么湍流模型。
然后你这个槽道,u+y+是某个点上的还是底面平均之后的?
另外,你试一下用这个方式来计算u+与y+
{ // Evaluate near-wall behaviour scalar nu = turbulence->nu()().boundaryField()[patchId][faceId]; scalar nut = turbulence->nut()().boundaryField()[patchId][faceId]; symmTensor R = turbulence->devSigma()().boundaryField()[patchId][faceId]; scalar epsilon = turbulence->epsilon()()[cellId]; // scalar omega = turbulence->omega()()[cellId]; scalar k = turbulence->k()()[cellId]; scalar magUp = mag(U[cellId] - U.boundaryField()[patchId][faceId]); scalar tauw = flowDirection & R & wallNormal; scalar uTau = ::sqrt(mag(tauw)); scalar yPlus = uTau*y[cellId]/(nu + rootVSmall); scalar uPlus = magUp/(uTau + rootVSmall); scalar nutPlus = nut/nu; scalar kPlus = k/(sqr(uTau) + rootVSmall); scalar epsilonPlus = epsilon*nu/(pow4(uTau) + rootVSmall); // scalar omegaPlus = omega*nu/(sqr(uTau) + rootVSmall); scalar Rey = magUp*y[cellId]/nu; Info<< "Rey = " << Rey << ", uTau = " << uTau << ", nut+ = " << nutPlus << ", y+ = " << yPlus << ", u+ = " << uPlus << ", k+ = " << kPlus << ", epsilon+ = " << epsilonPlus << endl; } -
感谢李老师关注。
你用的是层流模拟么,还是什么湍流模型?没看到你用什么湍流模型。
我用的湍流模型和channel395的一样,是
FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object turbulenceProperties; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // simulationType LES; LES { LESModel WALE; turbulence on; printCoeffs on; delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } PrandtlCoeffs { delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } smoothCoeffs { delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } maxDeltaRatio 1.1; } Cdelta 0.158; } vanDriestCoeffs { delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } smoothCoeffs { delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } maxDeltaRatio 1.1; } Aplus 26; Cdelta 0.158; } smoothCoeffs { delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } maxDeltaRatio 1.1; } }然后你这个槽道,u+y+是某个点上的还是底面平均之后的?
是底面平均之后的,postChannel工具会把槽道按照xz线(x和z坐标固定,y坐标变化)求平均,所以我使用postChannel输出的数据计算u+和y+,就是底面平均之后的。
-
这个方法的重点是那个应力张量吧
symmTensor R = turbulence->devSigma()().boundaryField()[patchId][faceId];我输出了wallShearStress,壁面切应力应该就是X方向的分量吧,和上面代码一个思路。能在paraview中看到上下壁面(patch)上的数据,话说做个平均应该就可以吧。顺便问下怎么做?
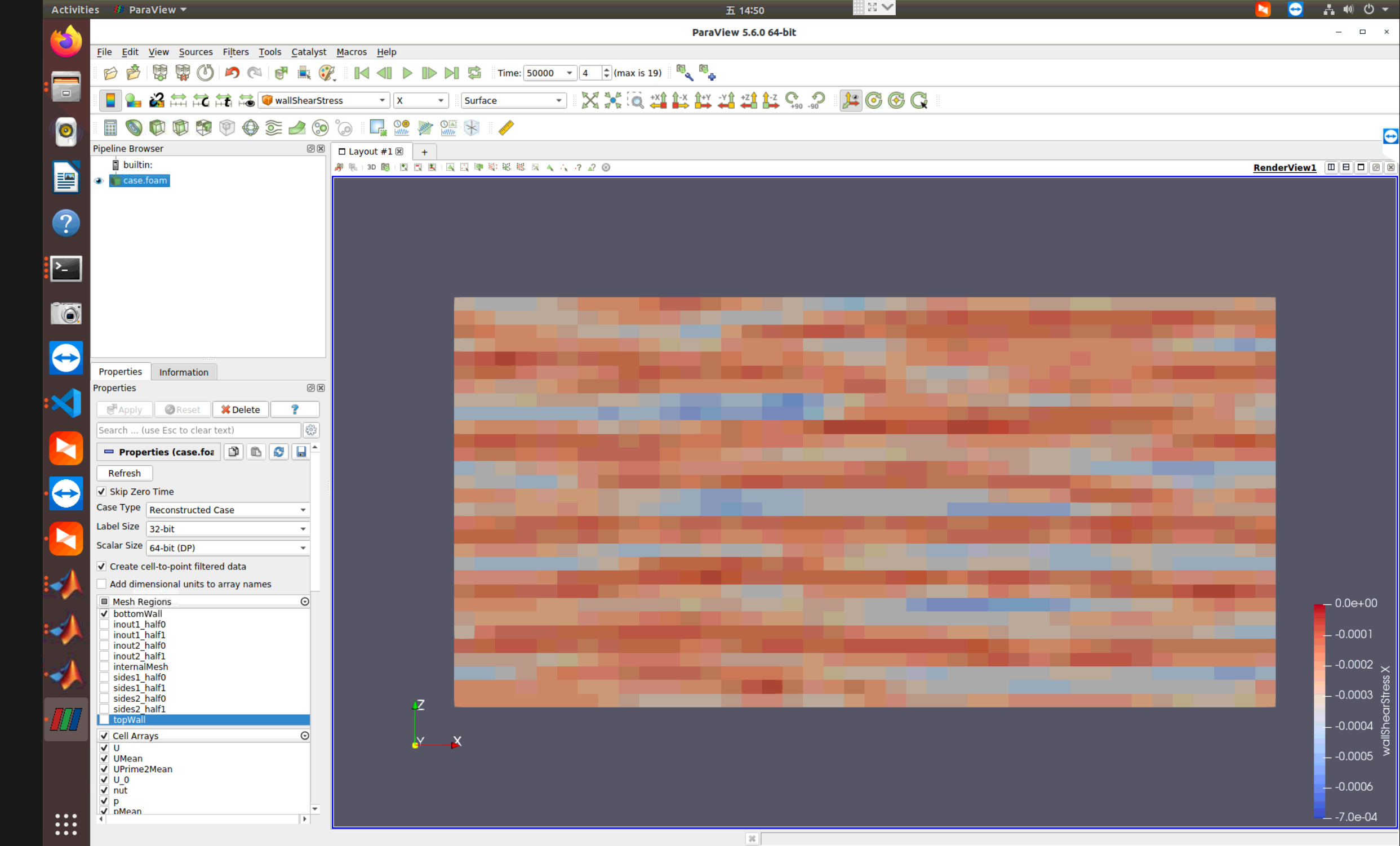
另外,wallShearStress计算出来的单位是(dimensions [0 2 -2 0 0 0 0];)也即m2/s2,而剪切应力的单位应该是(dimensions [1 -2 -2 0 0 0 0];)kg/m2/s2,刚好相差一个密度,所以OpenFOAM输出的wallShearStress还需要乘以密度,才是实际计算使用的剪切应力。
-
以OpenFOAM自带的channel395算例为例,我这里有4种计算$u_{\tau}$的方法。
方法一:
$$ u_{\tau } = {\rm Re}_{\tau }\nu/h=395*2e-5/1 $$
得$u_{\tau } = 0.0079000$。
方法二:
过计算出来的速度-高度曲线,实际地进行计算。$$ {u_\tau } = \sqrt {\nu {{\left. {\frac{{du}}{{dy}}} \right|}_{y = 0}}} = \sqrt {\nu {\frac{{u_1}}{{y_1}}}} $$
其中${u_1}$和${y_1}$分别是第一个输出点的流向速度和到壁面距离。
得到$u_{\tau } = 0.0069133$。方法三:
通过paraview的filter - integrate variables - 查看 cellData,得到wallShearStress的和以及面积Area,计算固壁面上的wallShearStress平均值,再使用$$ {u_\tau } = \sqrt {\frac{{{\tau _w}}}{\rho }} $$
计算摩擦速度$ {u_\tau }$。注意不可压缩求解器中没有密度,则认为$\rho=1$。
结果是$u_{\tau } = 0.0066952$。方法四:
在完全发展的槽道流中$$ \frac{{\partial p}}{{\partial x}} \times h = {\tau _w} $$
也就是 压力梯度 乘以 槽道半高 等于 壁面摩擦应力。给定平均速度的情况下,OpenFOAM会调节压力梯度使得平均速度达到设定值。在channel395的算例中到计算快结束时候,选择了某一时刻的压力梯度$\frac{{\partial p}}{{\partial x}} = 4.44604e-05$。代入计算,
得到$u_{\tau } = 0.0066678$。
你看这种方式计算出来的$u_{\tau }$跟你的区别大么
可以看到方法一是一种结果,方法二、三、四的结果很接近。
现在的问题就是实际计算出来的摩擦速度和由${\rm Re}_{\tau}$给出的摩擦速度不一样,但方法一的结果才是正确的。自带的channel395也对不上么?
channel395算例的结果
方法一的摩擦速度归一化结果是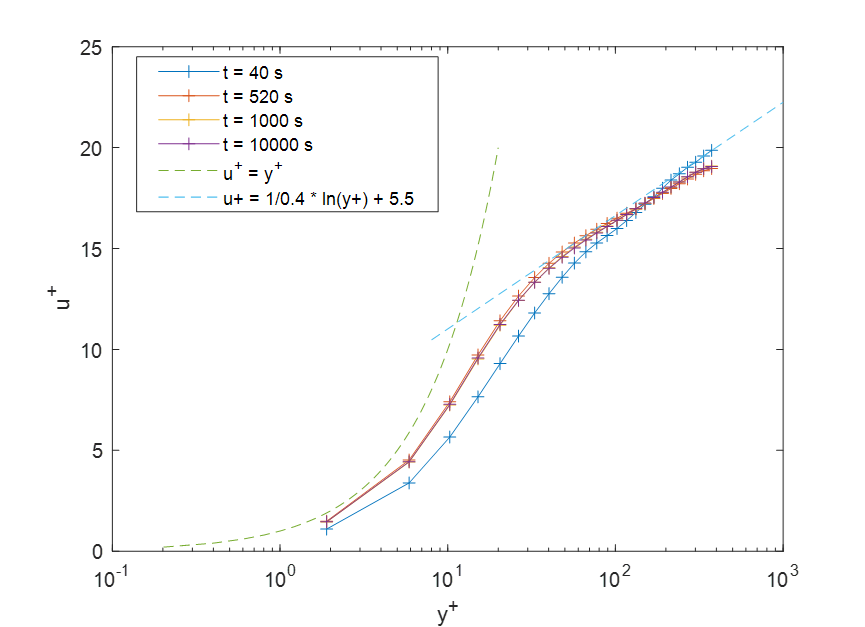
方法二(方法三和四也是这样子的图)摩擦速度归一化结果是
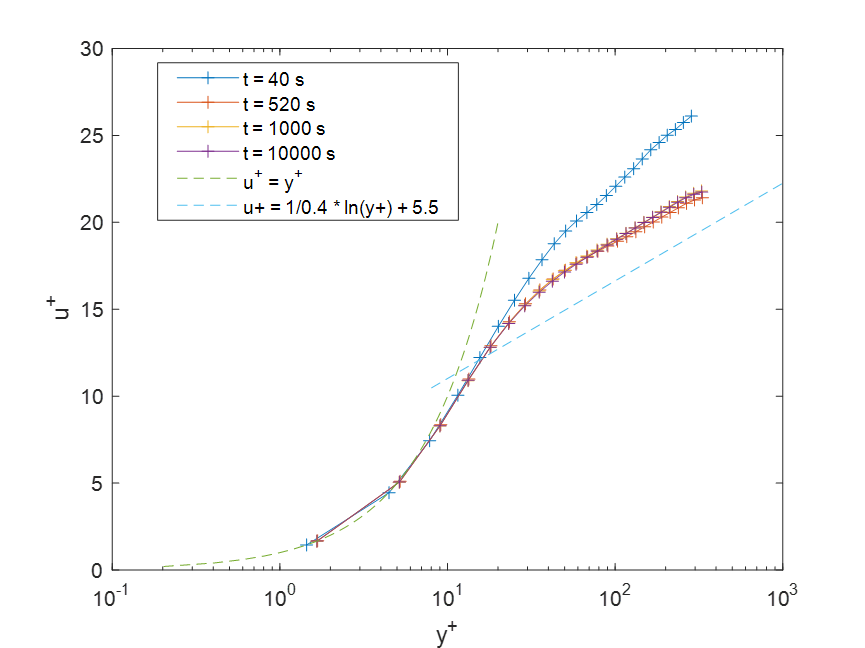
channel1000的结果在一楼。
现在感觉是槽道流动还是没算对。 -
channel395的平均yPlus是1.5910。channel1000的平均yPlus是0.8471。
channel395的fvScheme格式是下面这个,channel1000也没改fvScheme。FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvSchemes; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // ddtSchemes { default backward; } gradSchemes { default Gauss linear; } divSchemes { default none; div(phi,U) Gauss linear; div(phi,k) Gauss limitedLinear 1; div(phi,B) Gauss limitedLinear 1; div(B) Gauss linear; div(phi,nuTilda) Gauss limitedLinear 1; div((nuEff*dev2(T(grad(U))))) Gauss linear; } laplacianSchemes { default Gauss linear corrected; } interpolationSchemes { default linear; } snGradSchemes { default corrected; } wallDist { method meshWave; } -
对,我最开始做槽道流算例的时候,用的他的初始化流场的方法,不然一直算的都是层流。不过chanel1000的这个不用特地初始化也可以。
下面这个是我的channel1000的算例,LES,就是在channel395的基础上改的,OpenFOAM版本是v2012。Allrun脚本可以直接运行,画图用matlab文件夹里面的boundary_layer_profile_2.m就行,改一下要画哪个时刻的就行。
各位老师同学有兴趣可以算一算,看看是哪里出问题了。帮帮我吧🙏
https://jbox.sjtu.edu.cn/l/L1Asg4 (提取码:1234) -
@学流体的小明 你好,这个下载链接需要校内VPN,外校无法下载,想问下能提供个外校人员可下载链接吗?
对,我最开始做槽道流算例的时候,用的他的初始化流场的方法,不然一直算的都是层流。不过chanel1000的这个不用特地初始化也可以。
下面这个是我的channel1000的算例,LES,就是在channel395的基础上改的,OpenFOAM版本是v2012。Allrun脚本可以直接运行,画图用matlab文件夹里面的boundary_layer_profile_2.m就行,改一下要画哪个时刻的就行。
各位老师同学有兴趣可以算一算,看看是哪里出问题了。帮帮我吧🙏
https://jbox.sjtu.edu.cn/l/L1Asg4 (提取码:1234) -
@coolhhh @李东岳
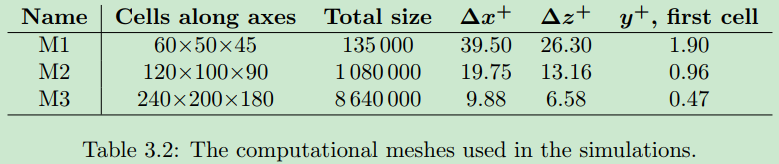
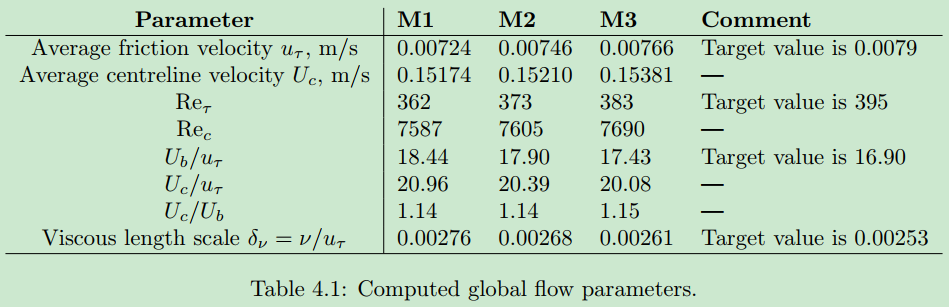
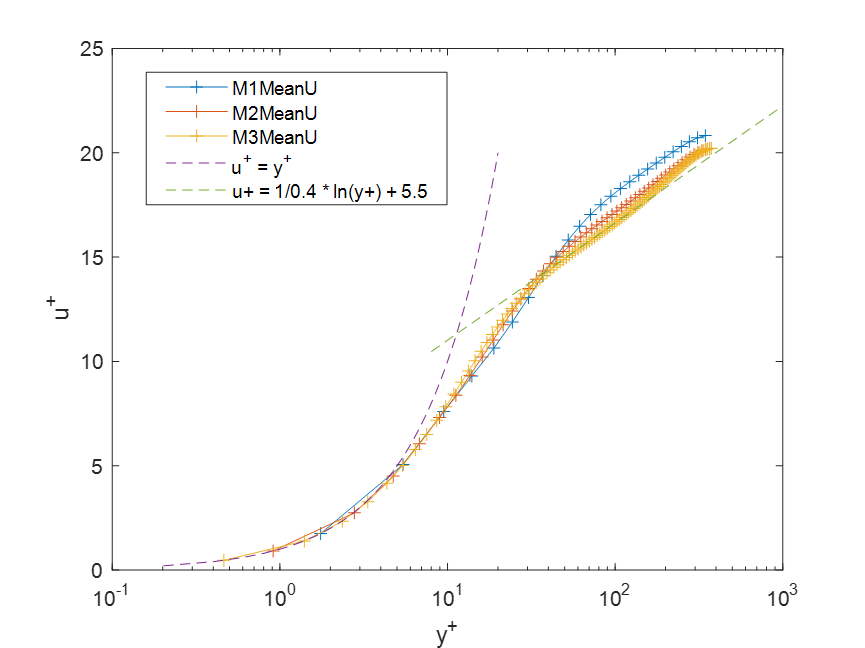
昨天仔细读了一下下面的这个文章,作者对OpenFOAM计算LES槽道进行了比较系统的分析。我发现他的图也是,只有最细的那套网格才算出了非常好的速度剖面,比较粗的两套网格都没算好,形状也和我的问题一样。
这篇文章还是在https://www.cfd-china.com/topic/2121/q-dns计算槽道流遇到了一些问题-求大神们指点看到的。之前读过,但是没仔细读😂。然后就浪费了好多好多时间。
确实是网格不够细的问题。https://www.sciencedirect.com/science/article/pii/S0021999117304059?via%3Dihub