Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam
-
换了计算域的形态,居然就能吻合得很好了。
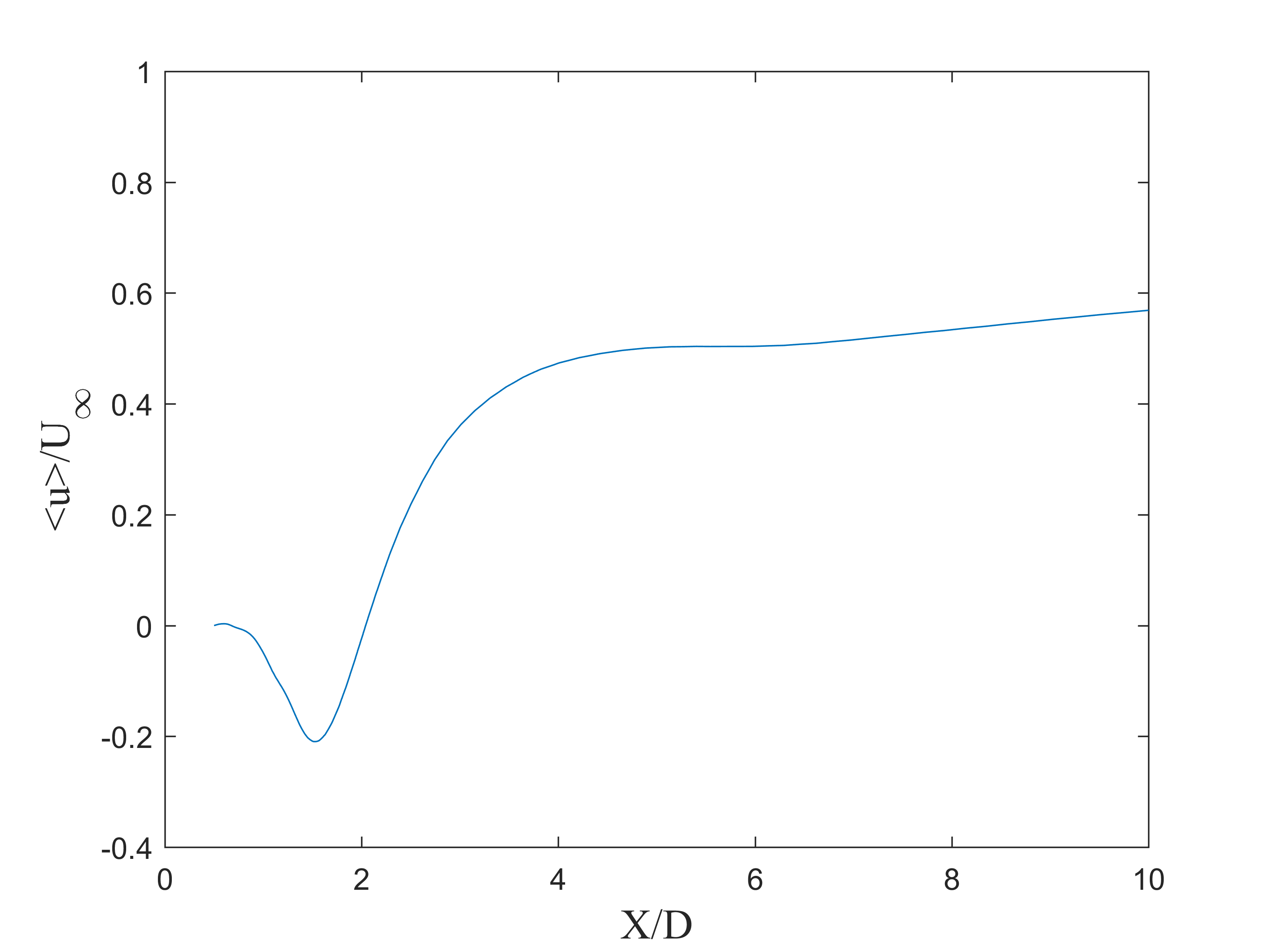
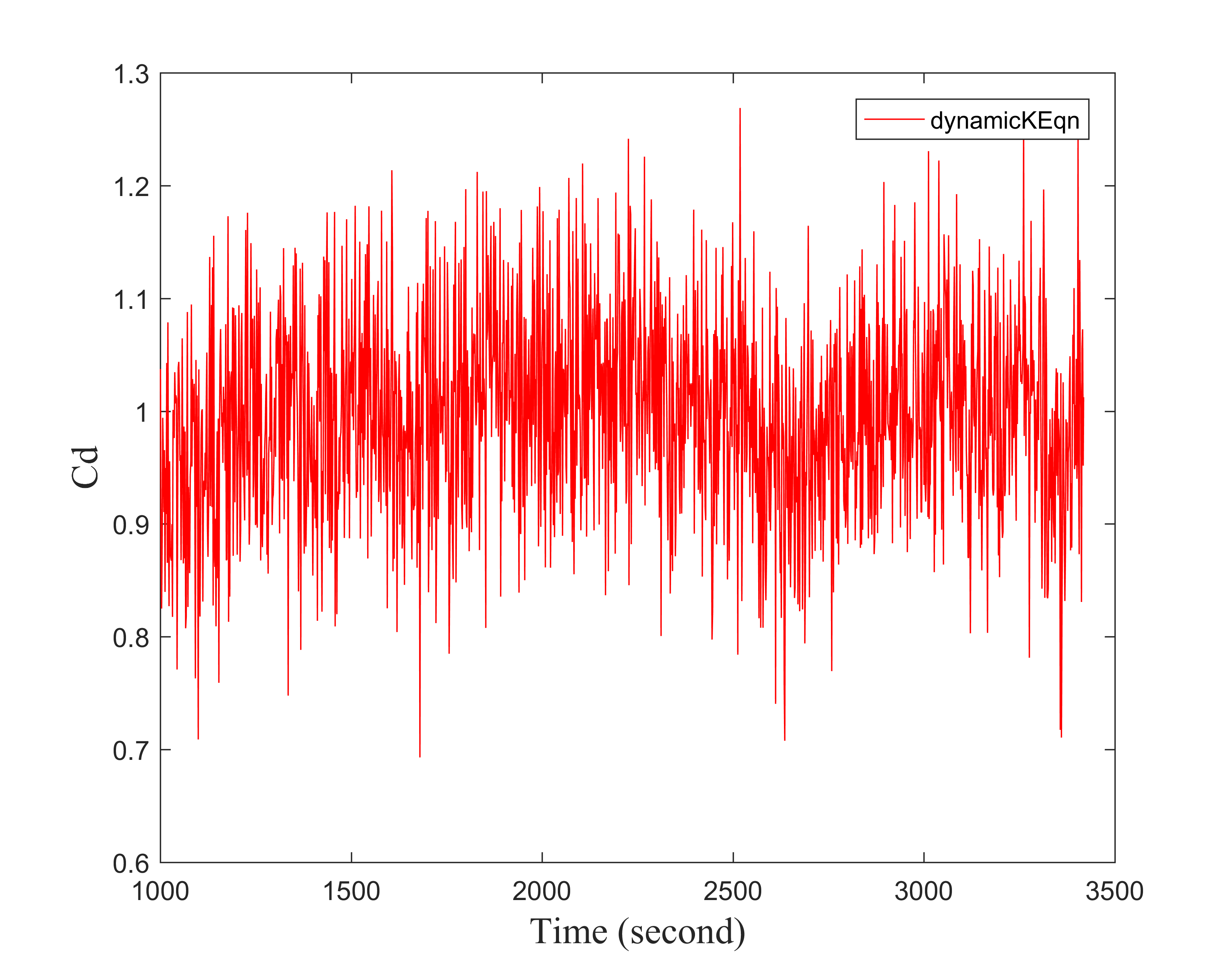
Cd 均值 1.03; St 0.21; Cl_rms 0.20; 30个周期96核,只用了12个小时;
可是为什么之前矩形计算域,算出偏高的数值?
难道雷诺数一样,不同的流体性质,也会对计算结果产生影响?

-
@random_ran 你这次只改了流场吗?你之前矩形的流畅有没有把过度的地方改一改,看看结果有影响吗?相同雷诺数,不同的流畅性质应该不会产生影响。
-
Hi yhdthu:
我的这个case没有重点关注涡量的绝对大小。主要考察的是平均Cd, Strouhal 数,recirculation的长度。 voriticiy 只是用三维等值面做了一下wake的结构。 不知道你的case 重点考察的对象是什么? 如果你能提供的一下你的涡量考察的座标,我可以把我的数据提供给你。
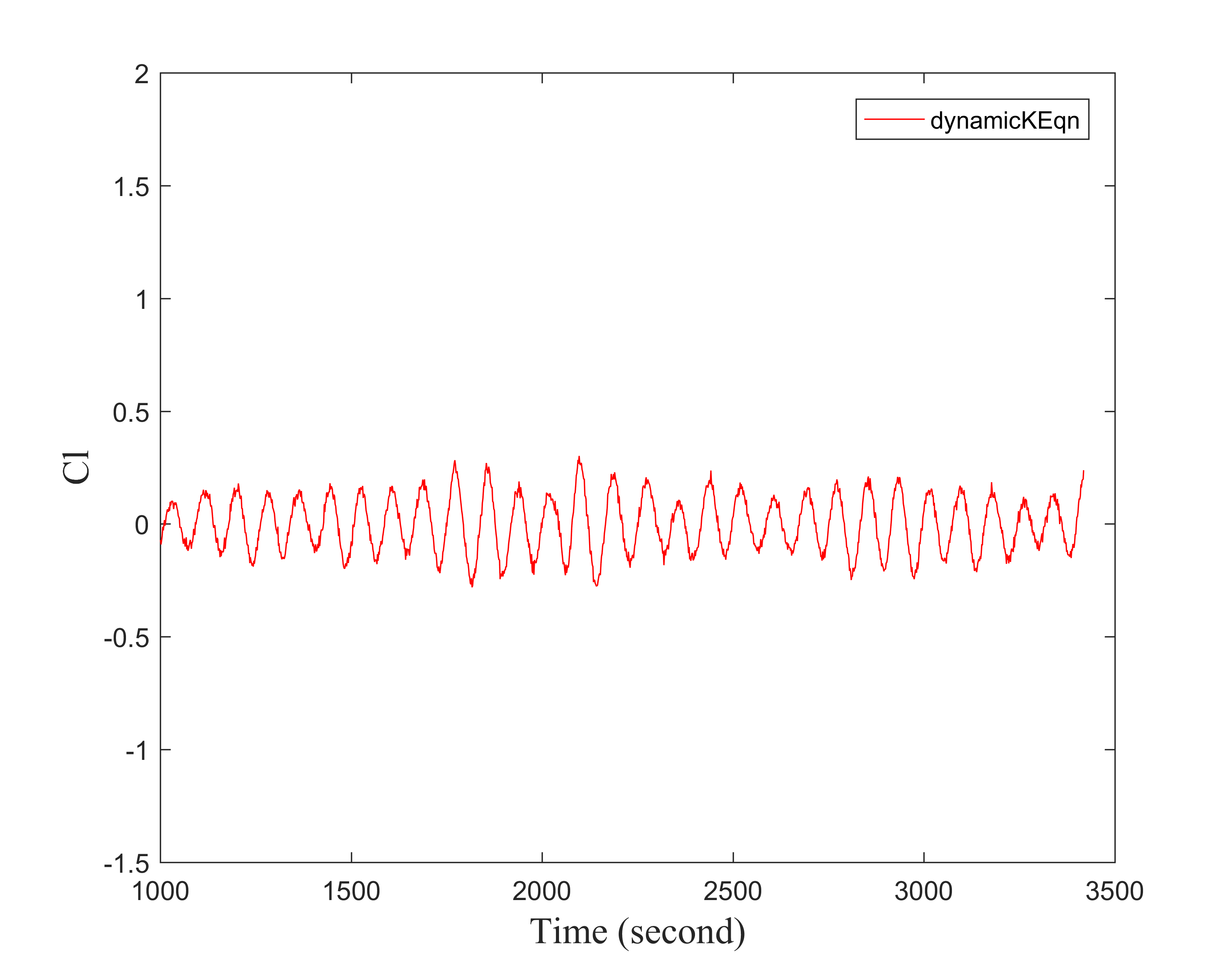
对于蓝色的线的Cd 我是把每个一个时间步长的Cd都输出来。这个Cd是平均的整个Cylinder的表面。 然后把每个时间点的Cd 对时间用matlab plot一下就是那张图了。
-
@random_ran
好的,谢谢你
第一个应该是用的DES模型计算的吧,我看帖子最上面的Cd随时间变化幅度很小,但是后面哪个用了动力模式做的Cd图波动很大,虽然均值基本上是和实验对得上的我的目的是想做空化模拟,但事前要先将湍流结构捕捉的较好才可以,目前二维试算用的是动力模式,Cd波动也很大,我不是每个时间步输出的结果,平均起来效果不是很好,可能是样本点太少了
可否将Cp曲线也po出来呢?还有其时间平均的定义,希望能做个参考,非常感谢
BTW,如果可以的话,加个微信好友,可以随时交流~358253794
-
最开始确实是DES。
dynamicKEqution的一大特点就是波动性,我第一次看到这个湍流模型运行出来的Cd历史的时候也被惊讶到了。可以参考:Lysenko, Dmitry A., Ivar S. Ertesvåg, and Kjell Erik Rian. “Large-Eddy Simulation of the Flow over a Circular Cylinder at Reynolds Number 3900 Using the Openfoam Toolbox.” Flow, Turbulence and Combustion 89.4 (2012): 491–518. Web.
如果湍流结果是一个前置条件的话,特别是你的雷诺数上千以后,2D的模拟总会计算出一个较高的Cd结果。 我不知道你是怎么计算Cd,O.F. 自己有专门计算Cd的object:
FoamFile { version 2.0; format ascii; class dictionary; object forceCoeffsIncompressible; }你可以按自己的需求调整输出频率。另外,文献中对采样点的多少也是各有各的看法。有的人(Franke 2002)采样150个周期(shedding period), 有的人(Kravchenko and Moin 2000)说采样10几个周期的结果和自己的实验结果很吻合,而更多的周期则会出现偏差。个人建议30~50个周期。
我这里有最开始那个DES的Cp图,传统的plot方法。后面的因为考察的方向不同,没有用传统的方式画,对你也没有参考价值。Lysenko 2012 年那篇里有Cp的plot,你可以参考他的。
Cp的做法,我是用ParaView 后处理得到的。先在OF设置好:在一个周期内,输出,比如20个点 (包含p,U场)。计算完成后在圆柱的中截面截取出压力值用来计算Cp (这个Cp是截面Cp值),这和Cd (整个圆柱)的算法是有区别的。得到了一个个的输出的时间点的Cp值之后,再对所有的采样的周期,比如30个周期,求出平均值。
ps 论坛的回复没有办法插入图片,如果你有需要我那个Cp,可以发我的邮箱.
个人习惯:不用微信以及一切即时通信软件。这是并行计算的哲学告诉我的:尽量减少cpu之间的通信以提升效率。 :joking:
-
@random_ran 好的,方法基本一致,我自己再整理一下,我觉得我的问题应该是后处理的问题,有问题再交流,祝好
-
近壁的地方是最难处理的,因为在这些地方没有大涡。LES也可以用wall function来避免太多的计算量,但是wall-resolved的LES的网格和DNS非常接近。
通常对壁面网格的控制是用无量纲墙距离 (yplus/y+)来标定。这个量的确定和雷诺数密切相关。对于wall-resolved的LES,y+<1是文献中最常提到的。对于用wall function的例子,y+可以放到30到200之间用来避免buffer layer,不同的wall function 还是有一些不同的要求。
对于stream-wise, span-wise,wall-resolved 的LES还有更高的要求。Georgiadis (2010)给出的建议是:
50< Δx+<150; Δy+<1; 15< Δz+<40
POINTWISE, NASA都给出了依据y+计算第一层网格高度的公式。
可以看看这个帖子。
-
方形计算区,o型网格覆盖3D~4D范围,再加上尾迹区加密,结果应该是一样的。主要原因,猜测是非正交网格对涡解析不够,造成Cd或Cl差异。至于涡对Cd和Cl影响,可以参考吴介之老师的涡动力学。
-
当时的计算结果高了大概10%~20%,当时试了很多:
Fixed grid jump transition area
Use LUST scheme for the convective terms
Implement LES turbulent models such as TKE and Smagorinsky model
Use nutLowReWallFunction instead of nutUSpaldingWallFunction
Increase computational domain
K and nut parameters
Boundary conditions: two cyclic with two slip wall conditions最后的结果发现换网格的效果是最好的。圆形计算域的正交性更好一些。而且这个计算域用自动生成都可以做到很好的质量,何乐而不为呢?
-
@Junhua-PAN 求书名,网上没搜到
-
@random_ran 想请教一个问题,如果用symmetry网格的话,对计算结果影响大吗?
