Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam

wwzhao

@yhdthu

我用wallGradU和面法向vector做内积就是我想要的分布了对不？

没错。

一直没搞懂用哪个滤镜

用 Contour 可以做 isosurface。

yhdthu

@wwzhao 多谢我试试～

random_ran

关于分离点的做法，重理一下思路。

流体在空间中运动，比较简单的情况下(比如沿A点流向B点)(不太严谨)，速度会减小, A点的静压力会高于B点的静压(伯努利方程)。我们说（p_B - p_A）> 0。也就是正压力梯度。

对于边界层出现流体分离的问题，比如我们研究的这个圆柱绕流问题。在边界层的一定区域，由于复杂的机理（暂时没想明白），出现了负压力梯度。这就意味着，在这个区域内的流体有向逆方向运动的趋势。从总体来看，流体是沿正方向流动。不过总会有一个瞬间一个时刻，这个逆潮流而上的部位，把这个部分的流体转向。在这个区域内，总有一个点的速度趋近与零。这个点就是分离点。

如何找到这个分离点呢？

现在把目光放在圆柱体表面，来研究沿圆柱表面法向量方向(指向流体)的速度分布情况。在没有分离出现的部位，我们沿法向量方向(指向流体)走一小步，速度会增大(从壁面表面出发的速度为零)。再考虑发生分离部分的流场，如果走同样的路径，你会发现速度同样会增大，但是速度的方向和之前正好是反向。如果考虑临界情况，就是说，当我们走出这一小步的时候，发现速度竟然没有变化！这个极限，就是分离点！如果把我们沿法向量方向(指向流体)走一小步并考察速度的变化，换成数学语言，就是du/dn=0的点！

接下来我再说说如何求这个点。

数学上讲，就是求速度沿壁面法向量的梯度。求梯度在ParaView可以通过
Filters-> Alphabetic->Gradient of Unstructured Dataset 对速度场进行处理，得到的是一个含有9个分量的二阶张量。但是这个并不是我们要求的沿壁面法向量的梯度。不过，还记得点乘(内积)的物理意义吗？如果用这个二阶张量”点乘” 法向量这个向量，不就得到了梯度在法向量那个方向上的大小了吗？

ParaView对速度场求梯度之后在每一个点得到了9个分量，从gradient 0 一直到 gradient 8。如果没有猜错，gradient 0 代表d(U_x)/dx, gradient 1 代表d(U_x)/dy, gradient 2 代表 d(U_x)/dz。这样的话用这个含九个分量的二阶张量点乘法向量，就可以得到速度梯度在法向量方向上的大小。计算方法如下：

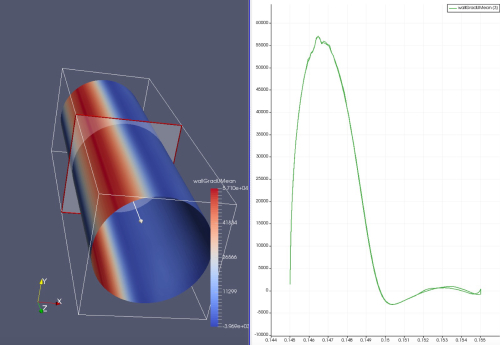
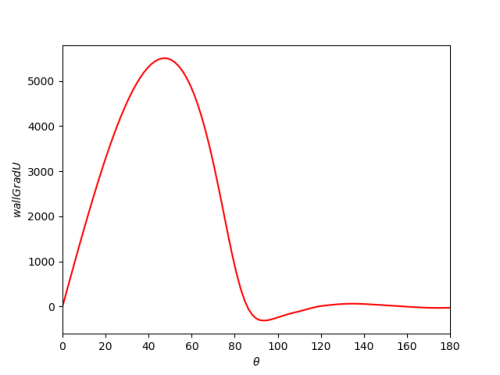
wallshearStress（成比例于速度沿法向量梯度，不是严格相等） = sqrt((Gradients_0*Normals_X + Gradients_1*Normals_Y + Gradients_2*Normals_Z )^2+(Gradients_3*Normals_X + Gradients_4*Normals_Y + Gradients_5*Normals_Z)^2+(Gradients_6*Normals_X + Gradients_7*Normals_Y + Gradients_8*Normals_Z)^2）

计算完成之后，得到的是一个标量。从这个图可以看出来过了极大值后，这个量开始骤降，第一次出现极小值点的地方，就应该是分离点了。

还请大家批评指正。

yhdthu

@random_ran 说得很好，我是通过修改wallGradU的代码实现的，直接给出了时间平均的值，不过在GradU为0的点后面的部分，需要人工手动加负号，体现速度方向相反，关键代码如下：

   wallGradUMean.boundaryField()[patchi] =
                    -UMean.boundaryField()[patchi].snGrad();

snGrand()就是面法向梯度方向了，显然这是个vector，mag一下即可

@wwzhao 这样看来，并不需要再乘以面法向向量了

yhdthu

@wwzhao 你好是不是这样：

-UMean.boundaryField()[patchi].snGrad() & mesh.Sf()

wwzhao

@yhdthu

被你搞晕了。。。说一下我是怎么分离点的吧。

修改wallGradU的代码，让它读取UMean，写出wallGradUMean。
得到wallGradUMean后，用paraview对圆柱表面的patch做slice，提取圆周上的点的wallGradUMean的值，保存到一个csv文件里。
用python写个脚本，读取并处理csv里面的数据，将wallGradUMean投影到圆周表面的切向方向。投影后的值出现正负变化的时候即为分离点。

yhdthu

@wwzhao 好的，我明白了，切向量是按着圆的切线方程得来的，这样上半圆与下半圆的切线方向是不同的吧？为了做出精确的曲线，在展向做切片的数量比较多如何处理？

wwzhao

@yhdthu

圆周上下是对称的，上下切一半即可。
对于展向切片较多的情况，建议你写个paraview的python脚本实现数据批量提取。

yhdthu

@wwzhao 你好我用你的方法试了，但是发现一个严重的问题，用paraview导出后的csv格式出现了数据丢失，比如我模型的x范围是(-1,1)，导出来之后区间缩小了，变成(-0.85,0.88)，请问这怎么处理呢？

wwzhao

@yhdthu 我没有遇到这个情况，你是怎么导出的？先做clip再做slice？

yhdthu

@wwzhao 我都试过，结果一样的，不知道怎么回事

random_ran

再仔细分析了一下计算，代码，和计算结果，又产生了疑惑。

疑惑的对象是：二阶张量点乘(内积,dot product)一个矢量，其结果应该还是一个矢量。这个点乘与两个矢量之间的点乘不太一样。后者结果是一个数。其物理意义是一个矢量在另外一个矢量方向上的投影长度乘以被投影到的这个矢量的模长。

那么这里的二阶张量点乘一个矢量得到的这个新矢量代表着什么呢？

这个新的矢量是否代表这着 du/dn, dv/dn 以及dw/dn?

那这个新矢量的物理意义就是某个点的速度沿法向量方向上的梯度？并不是我们要求的速度沿圆周面切线的分量沿法向量的梯度？

越绕越糊涂。

wwzhao

@random_ran 之前我的表述有误。这里不涉及到二阶张量，snGrad返回的是一个矢量，代表壁面处速度沿法向的变化率。由于壁面上的速度为0，所以snGrad返回的实际上就是第一层网格的速度除以第一层网格格心到壁面的距离。snGrad是平行壁面的，在二维情况下（+x为右，+y为上，流速指向+x），取圆周上半部分，当snGrad的方向由顺时针变为逆时针时（snGrad在顺时针切向方向的投影符号发生变化），即为流动分离点。

wwzhao

@yhdthu 你看的是"Points:0"，"Points:1"和"Points:2"吗？这个不是按大小排序的，仔细检查一下。

yhdthu

@wwzhao 你好，我是直接把点转化成了角度值，发现只有60度到120度

yhdthu

@wwzhao 你好，我有个新思路，是直接在of代码中改的，具体如下：

想办法求取每点的切向量，其方向在上下半圆都是流动的反向，之后与以UMean计算的snGrad做内积

实现这个切向量的方法很简单，就是用一个vector(0,0,1)与面法向量做叉积，再乘以面法向量在y轴的投影正负号函数

这是最后的效果图：

wwzhao

@yhdthu

这个是我的结果，纵坐标已经处理过，分离角85.8度。

random_ran

再顺思路：

将速度(矢量)沿切线(矢量)分解，求出切线速度(矢量)
对1所得切线速度（矢量）求梯度，得到含九个分量的二阶张量
用这个张量点乘法向量得到一个新的矢量，也就是切线速度沿法线上的梯度
将3中所得矢量点乘切线向量，最后得到一个标量
沿圆周画出4得到的标量，找到等于零的点对应的座标

这是目前基于O.F.直接计算结果，我能想到的计算分离角的方法。ParaView似乎对叉乘不太支持？这样第一步似乎就走不通了。还需要再研究。

看来不动O.F.代码真是麻烦了...

yhdthu

@random_ran 我改的代码如下，写的可能有点啰嗦，如果有更好的表达形式望告知

        forAll(wallGradUMean.boundaryField(), patchi)
        {
            const fvPatch& currPatch = patches[patchi];
            if (isA<wallFvPatch>(currPatch))
            {
                	
                wallGradUMean.boundaryField()[patchi] =
                    (
                    	-UMean.boundaryField()[patchi].snGrad() &
                    	(
                    		(
            			mesh.Sf().boundaryField()[patchi]
            			/mesh.magSf().boundaryField()[patchi]
                    		) ^ vector(0,0,1)
                    	)
                    ) * sign(mesh.Sf().boundaryField()[patchi] & vector(0,1,0));
            }
        }

random_ran

一种方法：

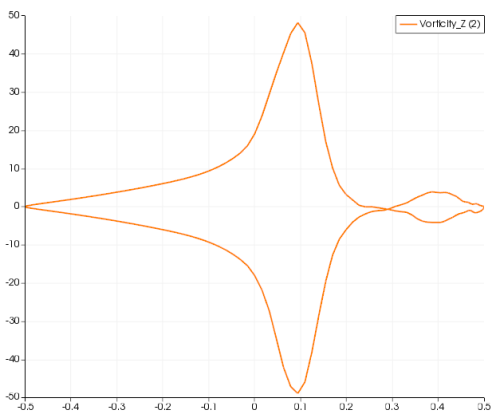
求出平均速度之后，用ParaView的 GradientOfUnstructuredDataSet 直接计算vorticity在Z方向上的分量. 不用动代码，只需要ParaView 5.2.0 版本以上。

CFD中文网

Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam