yPlus在openfoam代码里面的实现

Calf.Z-DNS

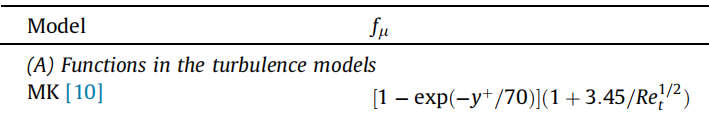
如果要植入MK湍流模型的话，里面有一项 47d6d46e-cba6-433f-89c2-6c135a81e936-图片.png
其中y+我按照了东岳老师提供的方法，那就是如下图：
42c137f7-26e2-4923-9c61-23be23c53c16-图片.png
编译成功，但按这个湍流模型跑的结果不对。

uTau为何设成1.003呢？如果要植入uTau的公式，那tauw这个如何得到呢？源代码里面相关的有tauw跟wallshearstress，但是不知道怎么引用。还望赐教。

李东岳

@Calf-Z-DNS 我那个是我自己写哒，计算出来之后是1.0003，具体我有点忘了下周回办公室给你看看

Calf.Z-DNS

@东岳好的谢谢！

Calf.Z-DNS

@东岳老师，请问uTau不应该用公式植入吗？在沿管方向的壁面上，uTau应该是变化的吧。如果用初始值计算出来的uTau定值植入，我试了下，湍流模型没有达到自己预想的效果。

李东岳

@Calf-Z-DNS 对，是用公式计算的，明天去办公室给你看看

李东岳

$u_\tau=\sqrt{\nu_t \frac{\rd u}{\rd y}}$

我在几年前看过有人做管道流动的温度DNS，非常酷炫，一直在关注你的结果，有好结果了发上来炫一波啊

Calf.Z-DNS

@东岳谢谢老师。uTau的公式我知道，但不用把这个公式植入代码里面吗？如果需要的话，有点不太清楚怎么写入代码，还望赐教。
DNS圆管的算例目前还在算呢，所需要的资源太大了，算比较慢。

李东岳

@Calf-Z-DNS

forAll(xxx, patchi)
{
    utau.boundaryFieldRef()[patchi] = 
        sqrt(nut.boundaryField()[patchi]*u.boundaryField()[patchi].snGrad());
}

李东岳

我之前见过一个视频，DNS模拟这种平板之间的浮力驱动流，最终里面的流体呈现这种弯曲的流线，这叫什么现象？最近打算复现一下这个东西

捕获.JPG

李东岳

@东岳 https://arxiv.org/pdf/1904.11400.pdf

Calf.Z-DNS

我做的压力驱动流，也是两个平板间的channel flow，上下有温差，但不考虑浮力。瞬时温度场长这样：
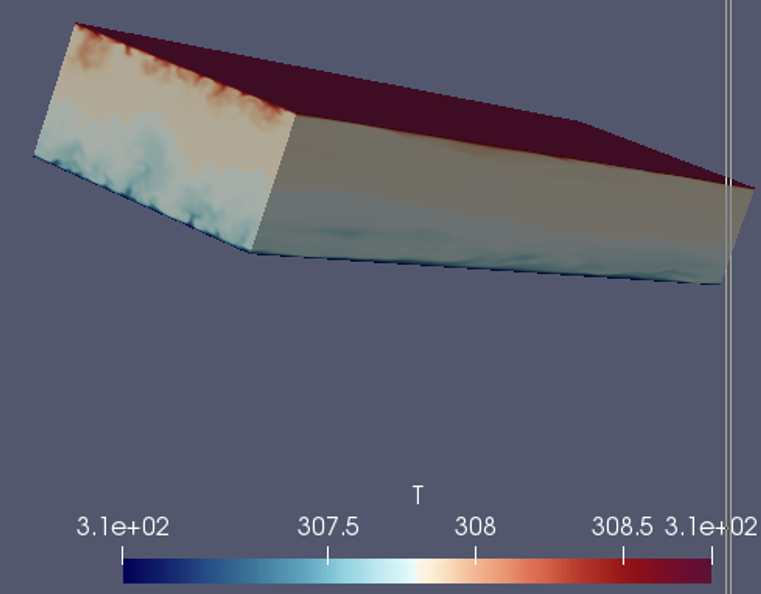
a6d9271b-0225-473d-9fa9-3d2938ba4216-图片.png

李东岳

你这个有弯曲的形状出来么？

本来打算这次OKS准备下这个模拟时间不够了，下次OKS准备一下，https://arxiv.org/pdf/1904.11400.pdf 主要是这个工况里面的流动感觉很有意思

Calf.Z-DNS

没有具体看流线，但我觉得应该是弯曲的，不过不清楚是否是规律弯曲的。

fangyuanaza

@李东岳请教下李老师~对于这里计算uTau，我用dimensionedScalar 是可以运算的，但是用这块代码计算uTau会报错，可能理解不太对。对于forAll中的×××，认为是uTau, 在这之前，我先定义了uTau是一个体标量场，初始值给的0，您代码中的u.boundary中的u认为是U.component(0)(), 这样代码能编译成功，但是运行几步会报错，请老师指教一下，万分感激(Ps 我在湍流模型里面实现这几个量，离壁面距离已经给出了，就是y_)：

    volScalarField u(U.component(0)());
    volScalarField uTau(0*sqrt(k_));
    //dimensionedScalar uTau("uTau", dimVelocity, 1.003);
    dimensionedScalar uTausmall(
       "0", dimensionSet(0, 1, -1, 0, 0, 0, 0), 1e-20
    );
    forAll(uTau,patchi)
    {
        uTau.boundaryFieldRef()[patchi] = sqrt(nut.boundaryField()[patchi]*u.boundaryField()[patchi].snGrad());
    }
    uadd_ = u/(uTau + uTausmall);
    yadd_ = y_*uTau/((this->mu()/this->rho_));

运行报错为：

#0  Foam::error::printStack(Foam::Ostream&) at ??:?
#1  Foam::sigFpe::sigHandler(int) at ??:?
#2  ? in "/lib/x86_64-linux-gnu/libc.so.6"
#3  Foam::sqrt(Foam::Field<double>&, Foam::UList<double> const&) at ??:?
#4  Foam::sqrt(Foam::tmp<Foam::Field<double> > const&) at ??:?
#5  Foam::RASModels::kOmegaSSTyuPlus<Foam::EddyDiffusivity<Foam::ThermalDiffusivity<Foam::CompressibleTurbulenceModel<Foam::fluidThermo> > > >::correct() at ??:?
#6  ? in "/home/dyfluid/OpenFOAM/OpenFOAM-7/platforms/linux64GccDPInt32Opt/bin/rhoSimpleFoam"
#7  __libc_start_main in "/lib/x86_64-linux-gnu/libc.so.6"
#8  ? in "/home/dyfluid/OpenFOAM/OpenFOAM-7/platforms/linux64GccDPInt32Opt/bin/rhoSimpleFoam"
Floating point exception (core dumped)

说是这个里面的sqrt传入变量不对？

xpqiu

@fangyuanaza 在 yPlus在openfoam代码里面的实现中说：

u.boundaryField()[patchi].snGrad()

u.boundaryField()[patchi].snGrad()

加上 mag 试试，也就是改成

mag(u.boundaryField()[patchi].snGrad())

fangyuanaza

@xpqiu 谢谢老师~按您这样修改以后，确实没有sqrt的错误了，但是还有错误没有解决：

#0  Foam::error::printStack(Foam::Ostream&) at ??:?
#1  Foam::sigSegv::sigHandler(int) at ??:?
#2  ? in "/lib/x86_64-linux-gnu/libc.so.6"
#3  Foam::RASModels::kOmegaSSTyuPlus<Foam::EddyDiffusivity<Foam::ThermalDiffusivity<Foam::CompressibleTurbulenceModel<Foam::fluidThermo> > > >::correct() at ??:?
#4  ? in "/home/dyfluid/OpenFOAM/OpenFOAM-7/platforms/linux64GccDPInt32Opt/bin/rhoSimpleFoam"
#5  __libc_start_main in "/lib/x86_64-linux-gnu/libc.so.6"
#6  ? in "/home/dyfluid/OpenFOAM/OpenFOAM-7/platforms/linux64GccDPInt32Opt/bin/rhoSimpleFoam"
Segmentation fault (core dumped)

#3应该是最关键的，但是学生不太理解的是编译的时候仅仅是在基本的kOmegaSST湍流模型修改的BasicTurbulencemodel，这里为什么会出现fluidThermo名称空间下的错误?

xpqiu

@fangyuanaza

    forAll(uTau,patchi)

这里有问题，按照这样遍历，你其实遍历的是每一个体网格，假设你有1000个体网格，那么 patchi 的范围是0-999，但是你接下来的代码是把 patchi 当成边界的编号来用，肯定不行的。至于为什么出现 fluidThermo下面的报错，那个是因为湍流模型有着一个复杂的继承关系，可压缩的计算所使用的湍流模型就会用到 fluidThermo 类相关的东西。

fangyuanaza

@xpqiu 理解了，因此我应该取uTau的边界网格进行遍历

    forAll(uTau.boundaryFieldRef(),patchi)

或者

    forAll(uTau.boundaryField(),patchi)

可以运行成功！但是这里对这种编程思路不太理解：
由李老师提供的公式来看，这里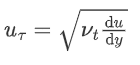
uTau应该是一个体标量场，这个值应该在近壁面是较大的，因为速度梯度较大，也就是边界层内部值比较大。那么为什么仅给网格边界赋值呢？而且，壁面上nut为零。如果只对边界进行赋值的话，uTau在壁面也是零。我输出uTau对比过了，uTau模拟出来结果在远场上边界才有值，其余地方为零，这是因为壁面nut为零，而场内部初始话赋予的零为初始值。

所以学生认为应该直接对整个网格场赋值。不知道理解对不对，请老师指点一下。

fangyuanaza

@xpqiu 请教老师，为什么不写成这样呢：

    forAll(uTau_, celli){
        uTau_[celli] = sqrt(nut[celli] * mag(tgradU()[celli].yx()));
    }
    uadd_ = u/(uTau_ + uTausmall);
    yadd_ = y_*uTau_/((this->mu()/this->rho_));

此处uTau定义为一个标量场。
是学生对这个公式理解不对吗？

xpqiu

@fangyuanaza
$u_{\tau}$ 应该是定义在壁面上的一个量，因为这个量跟壁面剪应力紧密关联，内部网格是没有壁面剪应力的。
首先，壁面剪应力的定义为
$$
\tau_w = \nu\frac{\partial u}{\partial y}
$$
$\nu$ 是分子粘度。
使用有限体积方法进行计算时，所有的计算都是离散的，因此
$$
\frac{\partial u}{\partial y} \approx \frac{u_{internal}-u_w}{\Delta y}
$$
$u_{internal}$ 表示第一层网格的速度，$u_w$ 是壁面速度，一般是0。
如果壁面附近网格画得很密（yPlus < 1），那么 $\frac{\partial u}{\partial y}$ 与 $\frac{u_{internal} - u_w}{\Delta y}$ 足够接近，因此这种情况下，壁面剪应力可以用
$$
\tau_w = \nu \frac{u_{internal}-u_w}{\Delta y}
$$

但是如果壁面网格画得粗，那么 $\frac{\partial u}{\partial y}$ 与 $\frac{u_{internal} - u_w}{\Delta y}$ 之间的差异就会很大。 OpenFOAM 的做法是利用 $\nu_t$ 来修正分子粘度，从而使得
$$
\tau_w \approx (\nu+\nu_t) \frac{u_{internal}-u_w}{\Delta y}
$$

回过头来看，其实不管是近壁网格画得粗还是细，都可以用上一个公式来计算 $\tau_w$ ，只不过壁面网格很细（ yPlus<1)时，可以认为 $\nu_t = 0$（但是 $\nu$ 不会等于0，所以壁面剪应力不可能为0，$u_{\tau}$ 也不可能为0）。而对于比较粗的网格，$\nu_t$ 比 $\nu$ 大得多，所以也可以认为 $(\nu_t + \nu) \approx \nu_t$，这应该也就是李老师写的公式的来源。

CFD中文网

yPlus在openfoam代码里面的实现