Smagorinsky模型系数问题
-
@李东岳 李老师,看
of2206中planeChannel算例的设置,LES采用Smagorinsky,提到设置Ce=1.048,Ck=0.0265463553,能够Updated to give Cs = 0.065。这里的Cs不太清楚对应哪个参数,但看官网上的符号说明,应该就是对应代码符号应该为Cdelta_。查看vanDriestDelta.C,Cdelta_为读取的参数,但of的算例数值为Cdelta=0.158。
问题:
(1)Cs与参数Ce和Ck的关系式是什么?
(2)Cdelta为读取的参数,如果要更新为0.065,那么是否要手动修改为Cdelta 0.065;而不是自动更新的?
of2206算例设置:/OpenFOAM-v2206/tutorials/incompressible/pimpleFoam/LES/planeChannel
LES { LESModel Smagorinsky; SmagorinskyCoeffs { Ce 1.048; Ck 0.0265463553; // Updated to give Cs = 0.065 } delta vanDriest; vanDriestCoeffs { delta cubeRootVol; cubeRootVolCoeffs { deltaCoeff 1; } Aplus 26; Cdelta 0.158; } printCoeffs on; turbulence on; }
OpenFOAM: User Guide: Van Driest

Cdelta_ ( dict.optionalSubDict(type() + "Coeffs").getOrDefault<scalar> ( "Cdelta", 0.158 ) ) -
我没太关注esi那面的版本,我看了下openfoam10,好像区别还挺大:
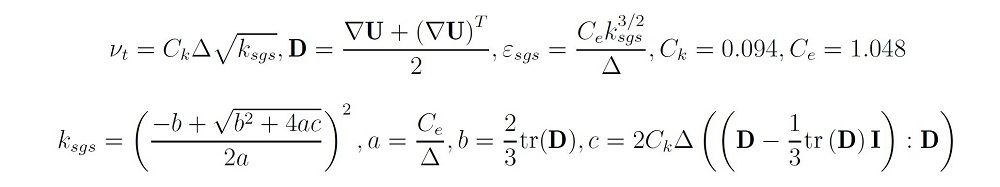
Description The Smagorinsky SGS model. Reference: \verbatim Smagorinsky, J. (1963). General circulation experiments with the primitive equations: I. The basic experiment*. Monthly weather review, 91(3), 99-164. \endverbatim The form of the Smagorinsky model implemented is obtained from the k-equation model assuming local equilibrium which provides estimates of both k and epsilon separate from the sub-grid scale viscosity: \verbatim B = 2/3*k*I - 2*nuSgs*dev(D) where D = symm(grad(U)); k from D:B + Ce*k^3/2/delta = 0 nuSgs = Ck*sqrt(k)*delta \endverbatim The default model coefficients are \verbatim SmagorinskyCoeffs { Ck 0.094; Ce 1.048; } \endverbatim -
@李东岳 李老师,ESI版本和org版本的
Smagorinsky和vanDriest基本是一样的。看了一些帖子,我把问题再总结一下:-
根据《Moin, P. and J. Kim, Numerical investigation of turbulent channel flow. Journal of fluid mechanics, 1982. 118: p. 341-377.》,建议取
Cs=0.065,而of中默认参数得到的不是这个值,需要调整Ck和Ce。

-
Ck,Ce与Cs的理论关系,可见《Sullivan, P.P., J.C. McWilliams and C. Moeng, A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorology, 1994. 71: p. 247-276.》。

-
根据下面两个帖子结论(帖子中是老版本的of代码),of中
Ck,Ce与Cs的关系与上面截图的理论公式一致。那么将of2206中的planeChannel算例设置用的Ce=1.048,Ck=0.0265463553代入,可得到Cs=0.065。
Smagorinsky model details -- CFD Online Discussion Forums ,
[转载]有关OpenFoam中LES smagorinsky模型的推导_馨予_新浪博客- 根据projectReport.pdf ,of中植入
vanDriest是将指数函数乘以过滤宽度实现,下面截图的公式感觉有点错误,应该改为:$\Delta = min \left [ \Delta_{mesh},(\frac{\kappa }{C_\Delta})(1-e^{-y^+/A^+})y \right ] $,这就与代码和官网上的写法一致。

- 问题:of的这种引入系数$\kappa, C_\Delta$的植入方式,目前还没找到相关出处,不知道为何要这么取值?同时官网上把$C_\Delta$写成符号$C_s$,所以在想$C_\Delta$是否与$C_s$是相同取值的?也就是说,设置用的
Ce=1.048,Ck=0.0265463553,可得到Cs=0.065,那么$C_\Delta$是否要设置为0.065?
-
-
我知道你什么意思了,老铁总结的太全面了,可以学习一阵子。
针对你的问题,应该就是我公众号发的那个。我也不清楚为什么OpenFOAM这么植入。有人说这样植入湍流产生与耗散会均衡。 -
感谢李老师分享,由于直接打开链接看不到评论区大佬的评论,我复制下大佬的观点:
1.


Straka Liu大佬推荐了一个非常有用的网站:Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION ,根据网站的推导,这两种方法是等效的,得到的$C_s$与Sullivan的论文公式是一致的:
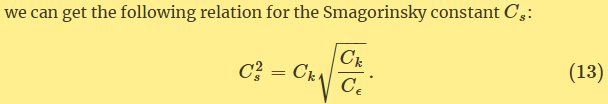
- 另外,Smagorinsky的开山之作《J. Smagorinsky, General circulation experiments with the primitive equations: I. The basic experiment*. Monthly weather review, 91(3), 99-164, 1963.》,大家现在能下载得到吗,我打开下载网站现在是
AMS Journals is unavailable
- 另外,Smagorinsky的开山之作《J. Smagorinsky, General circulation experiments with the primitive equations: I. The basic experiment*. Monthly weather review, 91(3), 99-164, 1963.》,大家现在能下载得到吗,我打开下载网站现在是
-
- 李老师,看评论区并根据Sullivan论文,第一种方法应修改为:$\nu _t =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $。评论区大佬说的是of中默认值
Ck=0.094, Ce=1.048,可以计算得到默认值Cs=0.167,这个数值是根据各向同性湍流的得到的。
-
我对湍流模型不太懂,但想到一个猜测观点:
(1) 如果用第一种方法指定$C_s$,根据$C_s=\left ( C_k \sqrt{\frac{C_k}{C_e} } \right ) ^{1/2}$,理论上反推的$C_k$和$C_e$就无法唯一确定,也就是说,一个$C_s$值是可以对应很多对$C_k$和$C_e$,比如采用Cs=0.065,那么可以取Ck=0.026546355, Ce=1.048或者Ck=0.04, Ce=3.585308638等很多组合。但可能第一种方法推导采用了ksgs的生成与耗散平衡假设,因此实际反算的$C_k$和$C_e$是与这种假设唯一相对应的。
(2) 如果用第二种方法,通过指定Ck=0.026546355, Ce=1.048,就可以唯一确定Cs=0.065。也就是说,可以动态指定$C_k$和$C_e$的取值对计算结果的作用程度,并且自然满足所预期的$C_s$。 -
结合下面这位大佬的评论,猜测第一种方法就默认ksgs的生成与耗散平衡,而第二种方法可以动态指定$C_k$和$C_e$,来反映ksgs的生成与耗散的非平衡关系?也就是第二种方法比第一种方法适用范围更广,当$C_k$和$C_e$能够取平衡状态的值,那么两种方法就是等价的?
- 李老师,看评论区并根据Sullivan论文,第一种方法应修改为:$\nu _t =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $。评论区大佬说的是of中默认值
-
1. 采用第二种方法:
(1)根据Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION的推导,基于式(5)的
Local equilibrium假设,对于incompressible flows,才能得到式(8)关系,进而得到式(10)和(11)。然后将式(11)与文献中的公式(12)对比,得到式(13)关于$C_e, C_k, C_s$三个系数的关系式。



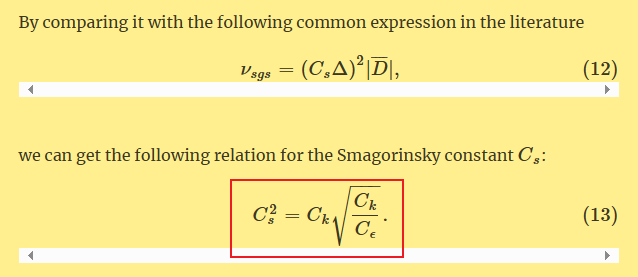
(2)现在分析式(10)和(11)。
-
首先这两个公式是基于
Local equilibrium假设得到的,将式(10)和(11)代入式(5),得到的结果自然满足Local equilibrium假设。 -
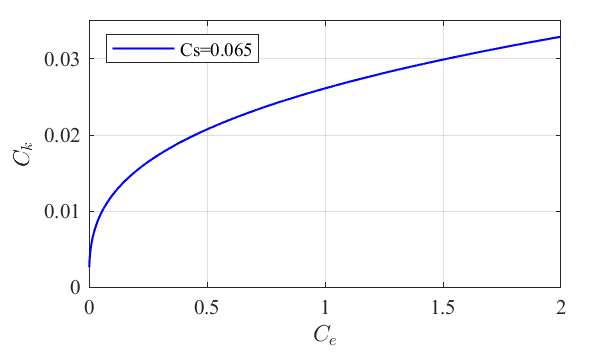
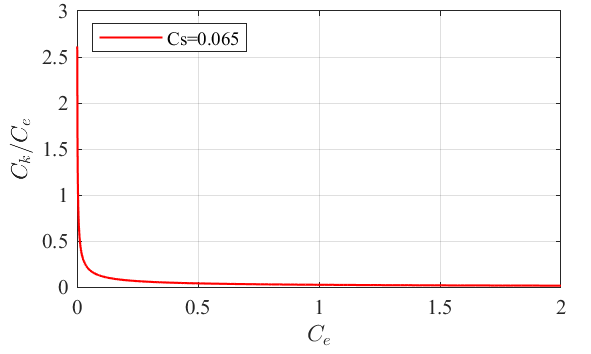
接着看式(11),我们可以通过设置合适的$C_e$和$C_k$,来实现等价的$C_s$。但是,式(10)中$k_{sgs}$的值与$C_k/C_e$这个比值相关联的。换句话说,计算设置满足了等价的$C_s=0.065$,但$C_k, C_e$可以有多种不同组合,这将导致$k_{sgs}$计算结果可能差别很大。根据式(13),可以得到:$C_k = \left ( C_eC_s^4 \right ) ^{1/3}$,以固定取$C_s=0.065$为例,画图如下。可以看出$C_e$取值越小,$C_k/C_e$比值变化越剧烈。表明了虽然结果都是满足
Local equilibrium假设以及实现了$C_s=0.065$,$C_e$和$C_k$仍然要取合适的组合,才能得到合理的$k_{sgs}$
2. 采用第一种方法:
个人疑问是植入:$ \nu _{sgs} =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $ ,
那么式 (1d) 中的$k_{sgs}$是怎么计算的?这会不会就是两个方法的主要差别?
-
-
我最近看到一个老版本的动态模型植入。植入的不是$\nu_{sgs} =\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $,而是$\nu_{sgs} =\left ( C_s \Delta\right )^2 \sqrt{ \mathbf{D} :\mathbf{D} } $,大佬怎么看
-
@李东岳 李老师, 这两个链接在讨论
of中的Smagorinsky模型时,也类似讨论of中为何植入的是$\sqrt{ \mathbf{D} :\mathbf{D} } $,相比理论公式看似缺少$\sqrt{ 2} $系数。但其实是一致的,这是因为of中把$\sqrt{ 2} $加到了前面的系数中。下面截图中的理论公式符号代表:$\left | \bar{S} \right | = \sqrt{2 \mathbf{D} :\mathbf{D} } $,但OF公式代表:$\left | \bar{S}_{of} \right | = \sqrt{ \mathbf{D} :\mathbf{D} } $,在CFD-online上的帖子因为把符号写成一样导致了混淆。
Smagorinsky model details -- CFD Online Discussion Forums
[转载]有关OpenFoam中LES smagorinsky模型的推导_馨予_新浪博客
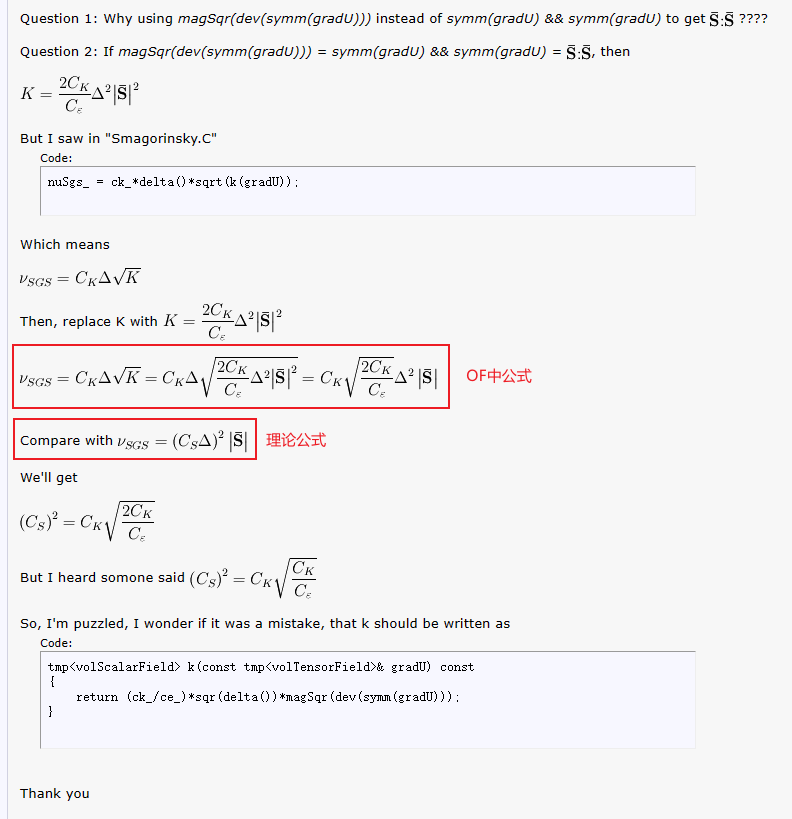
湍流模型我不太懂,在想
dynSmagorinsky是否类似于CFD-online的讨论,是否也是把系数$\sqrt{ 2} $加到了前面的系数中?也就是cD(D)可能比dynSmagorinsky理论公式多了$\sqrt{ 2} $系数?void dynSmagorinsky::updateSubGridScaleFields(const volSymmTensorField& D) { nuSgs_ = cD(D)*sqr(delta())*sqrt(magSqr(D)); nuSgs_.correctBoundaryConditions(); } -
@李东岳 这个公式结论是对的,不用加$\sqrt{2}$。CFD-online讨论帖子初始问题混淆点是把OF计算的$\sqrt{ \mathbf{D} :\mathbf{D} } $当做$\left | \bar{S} \right | $,而理论公式的$\left | \bar{S} \right | $表示的是$\sqrt{2 \mathbf{D} :\mathbf{D} } $。OF是单独计算了$\sqrt{ \mathbf{D} :\mathbf{D} } $,为与理论对应,$\sqrt{2}$在前面的系数里计算再相乘。
Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION这个帖子推导就没有混淆符号,统一用$\sqrt{2 \mathbf{D} :\mathbf{D} } $表示$\left | \bar{S} \right | $

-
 李 李东岳 被引用 于这个主题
李 李东岳 被引用 于这个主题
-
对,因为湍流模型不太懂,我猜测
dynSmagorinsky差个$\sqrt 2$可能是这个原因。Smagorinsky模型不是直接植入这个公式,是通过把系数代入$\nu_{sgs}=C_k\Delta \sqrt{k_{sgs}}$后得到等价的$\nu_{sgs}=C_k \sqrt{\frac{2C_k}{C_e} } \Delta ^2 \sqrt{\mathbf{D} :\mathbf{D} }
=C_k \sqrt{\frac{C_k}{C_e} } \Delta ^2 \sqrt{2\mathbf{D} :\mathbf{D} }=\left ( C_s \Delta\right )^2 \sqrt{2\mathbf{D} :\mathbf{D} } $