计算机图形学中的流体模拟为什么计算那么快，可否借鉴其优势。

Jerry

李东岳

我不太了解计算图形学的内容，据我了解算法不太一样。那面倾向于用拉格朗日算法。如果不用上亿的例子，拉格朗日算法不需要网格并且算法特别简单。CFD界之前专门发过一个文章，国外有一个教授专门玩这个。好像引用30000多了，CG那面流体模拟的

Jerry

@东岳谢谢李老师啦o(^o^)o

bestucan

有个开源软件blender，里面用格子玻尔兹曼方法做流体仿真。这个软件可以做动画，每年出一个小动画，一点没有开源软件手工作坊的感觉。

Jerry

@bestucan 哈哈哈，这个我见师姐用过，好像也可以做图形学的后处理😀

李东岳

还可以模拟类似DEM

李东岳

刚才看一个视频，那面一帧（如果调用三四百万粒子）大约需要120秒计算，电影一般30帧一秒钟，那么一秒钟大约需要40分钟计算，出1分钟的纯物质点算法的电影，需要计算40小时

https://www.youtube.com/watch?v=8iyvhGF9f7o

.J.

昨天看了清华姚班的一篇知乎文章，“99行代码的《冰雪奇缘》”，介绍他在MIT读博期间做的CG相关的成果。为了计算加速，手写了编译器，实在厉害。
原文：https://zhuanlan.zhihu.com/p/97700605?utm_source=qq&utm_medium=social&utm_oi=44817232953344

Samuel-Tu

计算速度相较于有限体积法快多少呢

李东岳

@Samuel-Tu 那面一帧（如果调用三四百万粒子）大约需要120秒计算，电影一般30帧一秒钟，那么一秒钟大约需要40分钟计算，出1分钟的纯物质点算法的电影，需要计算40小时。但是没有说他们用了多少核

如果纯拉格朗日粒子，可以用OpenFOAM的DPMFoam试试400万粒子的计算时间，看看用不用40秒

.J.

@东岳发现知乎那篇文章里提到，早期的物质点法计算速度也是很慢的，需要上集群才行。

李东岳

上午不知道在哪里看到了什么东西，找找找就找到计算图形学了，目前在游戏那面有一批人用的算法是基于Fast Fluid Dynamics（FFD），FFD主要用于天气预报那面。OpenFOAM创始人Weller的媳妇做这面就比较多。一般认为FFD算法起源于Stam, 1999, Selle, 2008。FFD算法非常简单，但是无条件稳定。%(#ff0000)[不管你用多大的时间步长，你就算去吧，never blow up。]很多讨论FFD算法的也把这个算法叫做Advection Projection Methods。

所有这些算法大体都是基于（类似操作符分裂）

求解纯对流：
\begin{equation}\label{con}
\frac{\p \bfU}{\p t}=-\nabla\cdot(\bfU\bfU)
\end{equation}
求解扩散+源（例如重力）：
\begin{equation}\label{diff}
\frac{\p \bfU}{\p t}=\nabla\cdot(\nu\nabla\bfU)+\bfg
\end{equation}
动量方程中还有压力项没有考虑：
\begin{equation}\label{p}
\frac{\p \bfU}{\p t}=-\nabla p
\end{equation}
把这个方程代入到连续性方程有压力方程：
\begin{equation}\label{poiss}
\nabla\cdot(\nabla p)=\frac{1}{\Delta t}\nabla\cdot(\bfU)
\end{equation}

在求解的时候，首先通过Semi-Lagrangian方法求解\eqref{con}，然后求解隐性的关于速度的泊松方程\eqref{diff}，然后求解压力泊松方程\eqref{poiss}，最后将压力代入到\eqref{p}获得divergence free速度。

FFD最主要的在于方程\eqref{con}，因为采用Semi-Lagrangian方法求解，因此没有库朗数限制，大幅度增加时间步长。注意：传统的欧拉方法处理对流项需要保证数值稳定行。Semi-Lagrangian方法类似粒子法，思想非常简单：如果网格1的速度以10m/s的速度向前传输，那么第10个网格点在1s的时候就是当前第一个网格点的速度。

在用有限体积法植入的时候，方程\eqref{diff} \eqref{poiss} \eqref{p}的计算都非常简单。但是Semi-Lagrangian方法要判断虚拟粒子的位置，可以通过OpenFOAM拉格朗日粒子包内嵌的算法实现（每个网格一个粒子）。连插值算法都有了。

捕获.JPG

FFD这种算法，属于一种先步进，后修正的策略（参考上图）。这也是为什么很多文章都叫做Projection方法的原因。但是在修正的过程中，由于Semi-Lagrangian可以调用很大的时间步长，因此对速度进行修正会引起误差（速度的平方即能量损失）。同时，Semi-Lagrangian在处理插值的时候，也会损失精度。参考 Liu et al. 的文章，下图是Semi-Lagrangian判断粒子在哪个网格位置的算法，其实就是Lagrangian的面寻址过程。

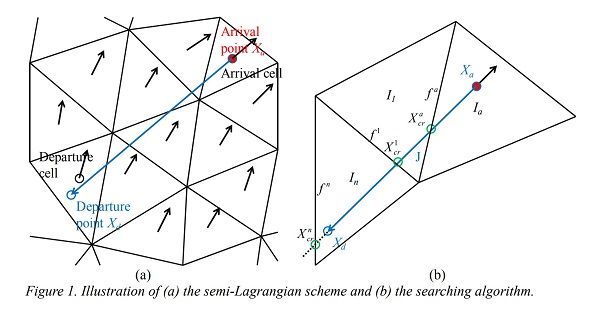
捕获2.JPG

Stam, 1999也声称：

Instead of their explicit Eulerian schemes, we use both Lagrangian and implicit methods to solve the Navier-Stokes equations. Our method cannot be found in the computational fluids literature, since it is custom made for computer graphics applications. The model would not be accurate enough for most engineering applications. Indeed, it suffers from too much “numerical dissipation”, i.e., the flow tends to dampen too rapidly as compared to actual experiments

FFD的核心在于Semi-Lagrangian算法，同时一些新的防止扩散的算法也有点新奇，这面主要用于Game，想拓展的研究领域的可以试试。没准以后可以去腾讯游戏，开发泥沙烟雾爆炸燃烧效果，年薪200万。

沙漠中的根

Jerry

@东岳李老师，这些英文文章您一般都从哪里下载的，我用学校的网也没法下载。

李东岳

@Jerry https://www.jianguoyun.com/p/DeI2Qt4Q9s3ZBhjho_AC

Jerry

@东岳谢谢李老师o(^o^)o

Hungryandfool

@J 把你最近学习的成果总结一下，发上来嘛

CFD中文网

计算机图形学中的流体模拟为什么计算那么快，可否借鉴其优势。