Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam
-
@random_ran 在 Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam 中说：
时的计算结果高了大概10%~20%，当时试了很多：
Fixed grid jump transition area
Use LUST scheme for the convective terms
Implement LES turbulent models such as TKE and Smagorinsky model
Use nutLowReWallFunction instead of nutUSpaldingWallFunction
Increase computational domain
K and nut parameters
Boundary conditions: two cyclic with two slip wall conditions
最后的结果发现换网格的效果是最好的。圆形计算域的正交性更好一些。而且这个计算域用自动生成都可以做到很好的质量，何你对比的是啥文献，用的什么边界条件呀？
我看有个早期文献是用FVM加变换算的无穷大边界的，和一般的有限大小边界还不一样。
如果你考虑正交性，你在fvScheme中加修正了么？梯度用的啥？OF对非正交和skew都有相应的修正方法，可以提高一点儿精度。我写过一个小帖子OF修正小结，你可以尝试搞搞边界条件类型和fvScheme中的修正。
-
主要参考的是
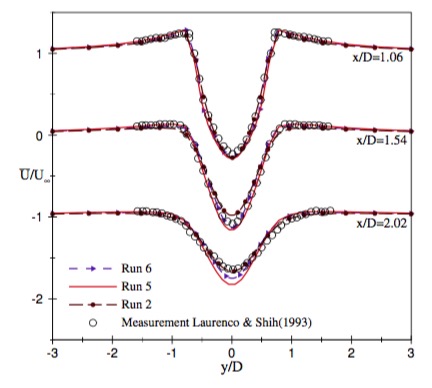
Lysenko, Dmitry A., Ivar S. Ertesvåg, and Kjell Erik Rian. “Large-Eddy Simulation of the Flow over a Circular Cylinder at Reynolds Number 3900 Using the Openfoam Toolbox.” Flow, Turbulence and Combustion 89.4 (2012): 491–518. Web.Lysenko (2012) 用的是：
- inlet: 层流
- outlet: wave-transmissive conditions （不太明白，我用的是 pressure:fixValue=0）
- span-wise: periodicity
- cylinder: no-slip
能提供一下那篇早期文献吗？
当时没有考虑正交性问题, 关于梯度的离散是这样设置的:
gradSchemes { default Gauss linear; grad(nuTilda) cellLimited Gauss linear 1; grad(U) cellLimited Gauss linear 1; }这个贴子当时是在算Re3900的时候遇到Cd的过高估计，最终发现换一套网格和用dynamic kEquation 就能把Cd预测的很准了，所以那段研究就没有再进行下去了。
有时间我会再把以前的那套网格用你提供的方案再算算，看看结果会怎么样。
-
@random_ran
waveTransmissive类似特征边界条件，反正Wikki是这么说的。可能更加有物理意义吧。 -
-
已婚，勿扰。
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 -
Yours in CFD,
Ran
-
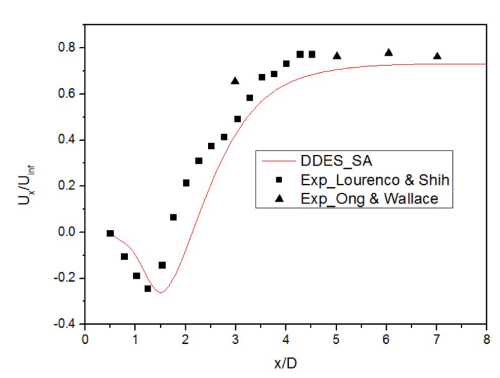
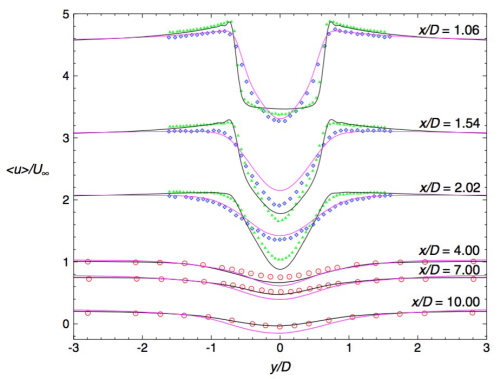
@random_ran 你好，我的意思是纵坐标其实没有实际意义，可以想象，在y/D>=3时，Ux=Uinf，所以文献给出的其实是示意图，是为了方便说事。
另外，我用的就是方形计算域，大概是220W，壁面附近特殊处理了一下，分成三个增长率生成网格，过渡区网格注意了一下。基于升力的St大概是0.202，Cd约为1.02，下次在电脑旁我会把其他参数加上。
对流项离散LUST，就是那个75%CD，25%UD
DES类湍流模型，DDES_SA -
wallShearStress可以在计算完成后处理，O.F. (v4.1)是有这个功能的，但是个人觉得这个没法找到分离点的座标，只是给出了应力的最大和最小值。
simpleFoam -postProcess -func wallShearStress在分离的地方，圆柱表面的剪切应力应该很接近零。不过一个点的剪切应力应该有三个分量，是考虑某个分量上的最小值还是合成的最小值？我也在想这个问题。
不过wallShearStress是和壁面速度沿壁面法向的梯度，所以用这个梯度也可以来求分离点的位置。结合ParaView是很容易实现的。
我建议还是用ParaView 后处理。
Filters-> Alphabetic->Gradient of Unstructured Dataset 对速度场进行处理。
然后用 Plot on intersection curve 输出圆柱表面的梯度分布，再输出所有时间步长的数据，就可以求出时间上的均值。如果在多切几个不同的界面，就可是实现空间上的均值。
希望能帮助到你。
-
-
-
-
希望讨论能把这些疑惑逐渐拨开。
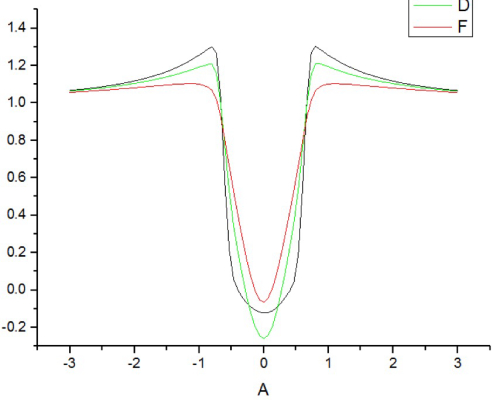
wallShearStress和近壁wall-normal的梯度成比例关系，所以 du/dn=0 的点就是wallShearStress为零的点。公式du/dn=0 中u指得是平行于壁面的速度，而n是壁面指向流体的法向量。三维问题不好描述，先在二维平面讨论。
假如我们考察圆周上(此时我们在二维平面内)任意一点A。A点处的速度在x轴和y轴（直角座标，原点在圆心,3点钟方向是x轴正方向,12点方向是y轴正方向）必有两个分量。但我们关心的是A点处的切向速度的大小：
$$ \v_{\tau} = v \cdot \tau) $$ 。
有了切向速度之后，在A点对这个速度沿A点指向流体的法向量求偏导，就可以得出在A点处平行于壁面的速度沿该点处壁面法向量的偏导。 (感觉很拗口，不知道这样理解对不对)
然而实际用ParaView来计算的时候还是有疑惑。
- 我知道如何求法向量(normal vector)，切向量怎么求？
- 假如我求出了切向量并得到了切向速度大小，是否就可以直接求出在A点处平行于壁面的速度沿该点处壁面法向量的偏导，而不是这个速度分别沿x,y的偏导？
最初的想法其实很简单，用 Filters-> Alphabetic->Gradient of Unstructured Dataset 对速度场进行处理。处理完后得到一个2阶张量，这个二阶张量没有直接给出在A点处平行于壁面的速度沿该点处壁面法向量的偏导。但是直觉告诉我，这个2阶张量经过一定的"变换"是可以得到在A点处平行于壁面的速度沿该点处壁面法向量的偏导。
越来越把自己绕进去了。寻求大家的帮助。
-
$\nabla \mathbf U \cdot \mathbf n$=grad(U)*normal吧
