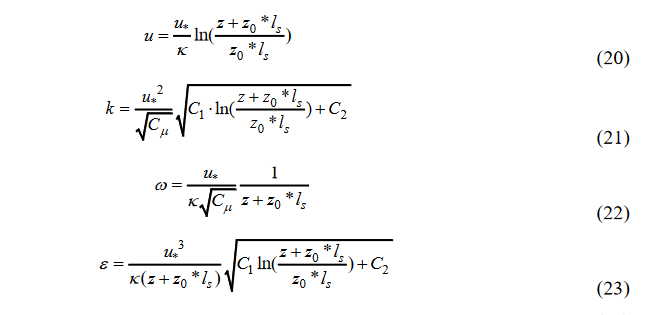中性大气环境湍流动能的自保持 | 附有算例下载
-
@李东岳 李老师,我重新看了下原论文,做了些测试:
1. Yang2009论文中
k剖面是缩尺的风洞拟合结果,不能用于全尺寸。Yang2009论文中k剖面,随着高度在增加如下所示。
2. 缩尺风洞目标值换算为全尺寸
(1)缩尺风洞目标值换算为全尺寸,要考虑缩尺比,包括:
几何缩尺比($S_L=L_{model}/L_{full}$),速度缩尺比($S_V=V_{model}/V_{full}$),时间缩尺比($S_T=T_{model}/T_{full}=S_L/S_V$)。
(2)对数率平均风、湍动能、耗散率剖面:
$$u=\frac{u_*}{\kappa}\rm{ln}(\frac{z+z_0}{z_0}) \tag{1}$$$$k=\frac{u_*^2}{\sqrt{C_\mu}} \sqrt{C_1\rm{ln}(\frac{z+z_0}{z_0})+C_2} \tag{2}$$
$$\epsilon=\frac{u_*^3}{\kappa (z+z_0)} \sqrt{C_1\rm{ln}(\frac{z+z_0}{z_0})+C_2} \tag{3}$$
从缩尺换算到全尺寸,需换算的参数:$u_* /S_V$,$z_0 /S_L$
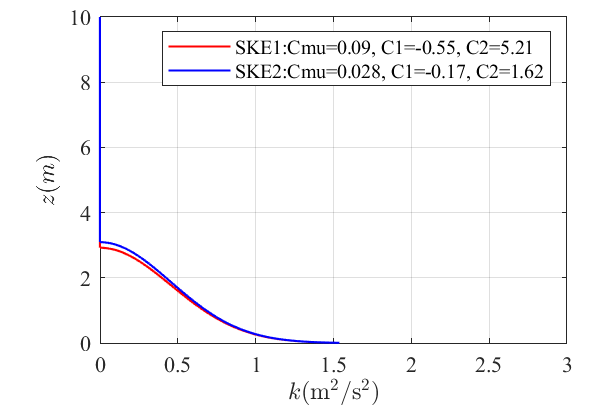
(3)Yang2009原论文中的风洞试验拟合结果如下,其中$k/u_* ^2$剖面沿着高度的均值等于2.86(SKE1)和2.91(SKE2)。
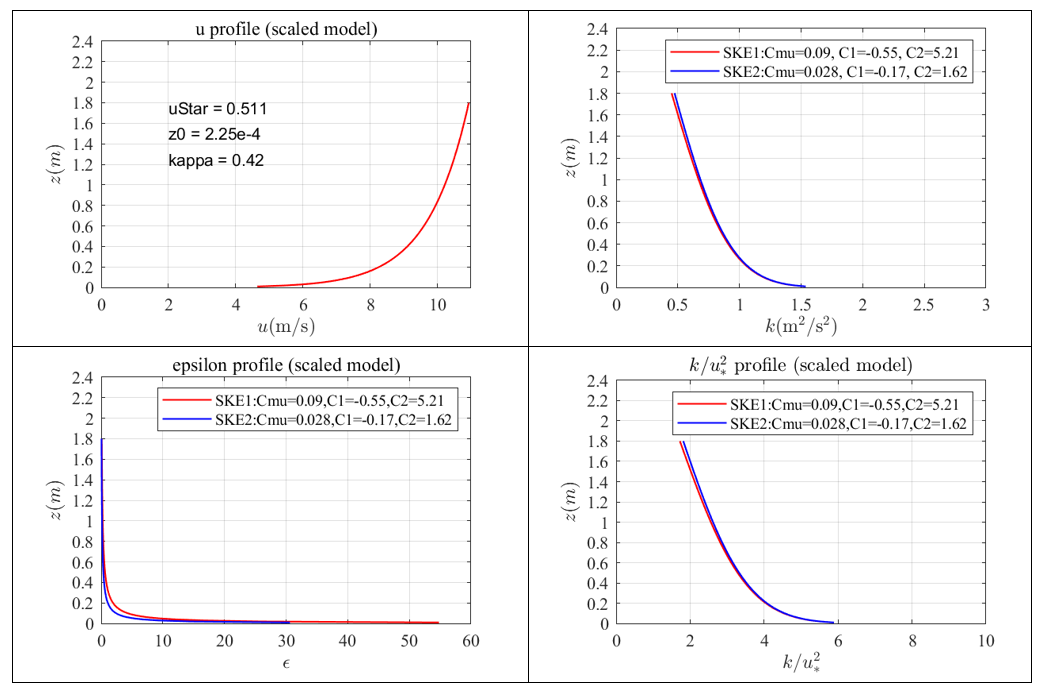
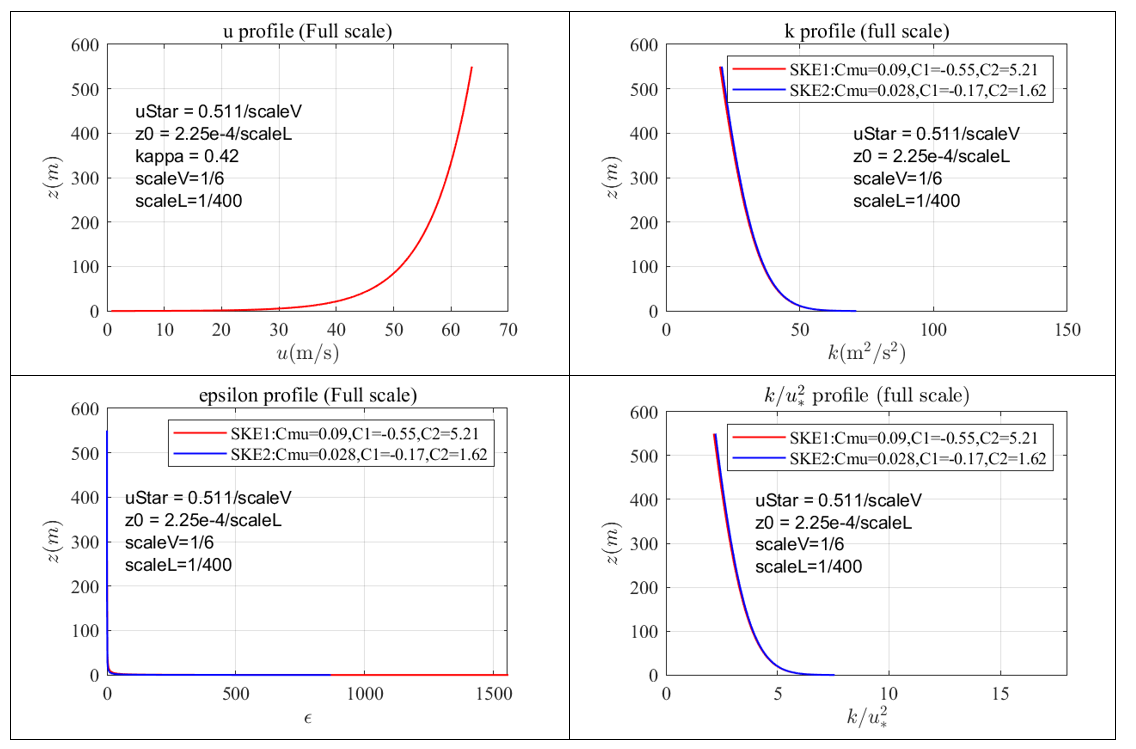
(4)假如取$S_L=1/400$,$S_V=1/6$(风洞试验10m/s,全尺寸取60m/s),对Yang2009论文的结果放大为全尺寸结果如下,其中$k/u_* ^2$剖面沿着高度的均值等于3.17(SKE1)和3.22(SKE2)
3. 对上述全尺寸的参数,进行RANS模拟
(1)对原算例网格每个方向都放大400倍(of9写法与of8不一样 )
# transform to full scale runApplication transformPoints "scale=(400 400 400)"(2)原算例设置算全尺寸会发散,修改
fvSchemes,增加grad(U) cellLimited Gauss linear 1;:gradSchemes { default Gauss linear; grad(U) cellLimited Gauss linear 1; }(3)0文件夹的U、k、epsilon对应修改为全尺寸参数
算例下载链接为:Yang2009FullScale_20230610.zip ,用of9执行Allrun或Allrun-parallel(4)模拟结果如下,平均风剖面不变,但k基本衰减为0。
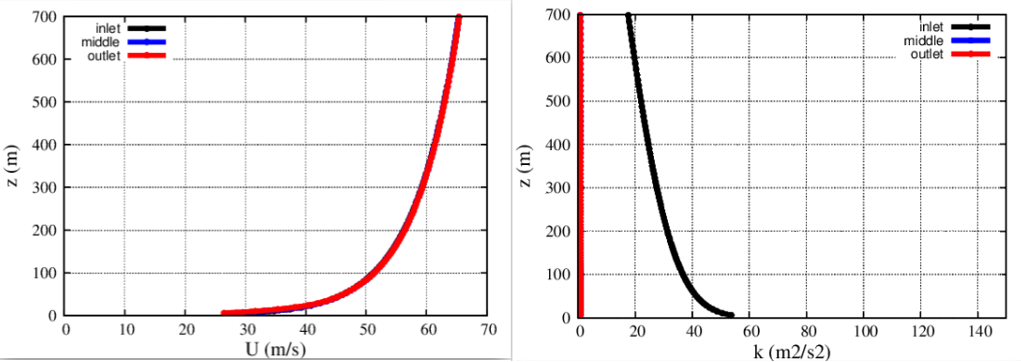
4.分析与疑问
(1)Yang2009原论文提到,参数 $k/u_* ^2$是根据风洞试验测量得到,具体是如何通过$k/u_* ^2$计算得到$C_\mu$?

(2)SKE1和SKE2模型,参数$C_\mu, C_1, C_2$组合都能很好的拟合实验结果,但RANS模拟自保持结果差别很大,其中$C_\mu$感觉像是重要影响参数。问题同(1),如何根据不同目标值,合理确定$C_\mu$?
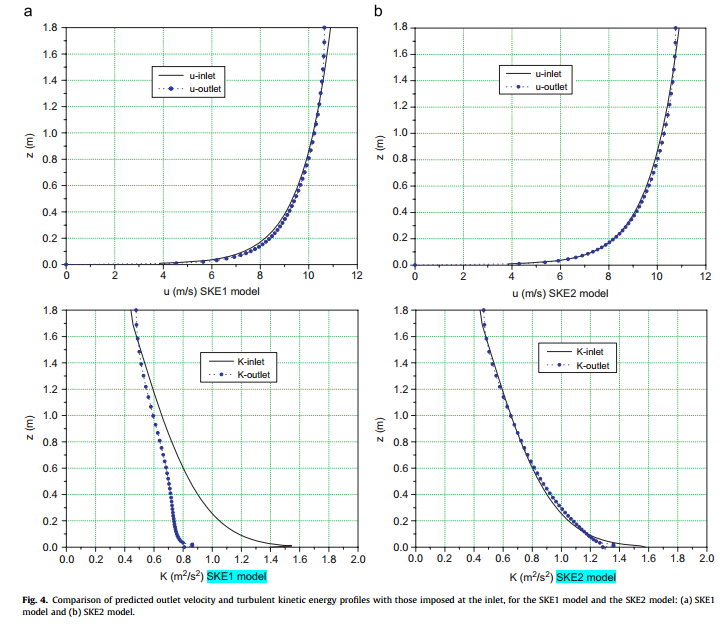
(3)全尺寸模拟的
k完全无法自保持,猜测原因:
①直接用缩尺目标值放大为全尺寸,参数组合$C_\mu, C_1, C_2$可能不一定适用。
②数值格式对全尺寸网格耗散更大,耗散程度对于网格尺寸增加成非线性增加的关系。但也尝试过把每个方向网格加密一倍,145万网格的算例结果也是跟上面的工况一致,k基本耗散为0
(4)OpenFOAM中提供的壁面函数,是否可用于全尺寸模拟?目前壁面函数的经验公式基本都是实验拟合出来的,虽然是无量纲化的。但能否用于全尺寸仍有待确定。本工况按原网格直接放大400倍,$y^+$值达到了2000~70000,这个数值对于全尺寸是否合理?
# y+ () # Time patch min max average 1000 top 2.315308e+01 2.312809e+05 4.448700e+03 1000 bottom 4.092494e+04 4.498426e+05 7.201201e+04 1000 sides 4.473468e-01 2.178080e+05 2.860156e+03
(5)HW07模拟结果,
k剖面的数值只有1.3左右,对于全尺寸而言这个数值是否太小不合理?如果HW07也模拟同样的目标值,结果会如何?@李东岳 在 中性大气环境湍流动能的自保持 | 附有算例下载 中说:
我在OpenFOAM里面植入了一个新的算法。我也把相关的内容更新在了《无痛苦NS方程笔记》。这个方法简称HW07,参考的是
D.M. Hargreaves and N.G. Wright 2007,目前这一套方法计算出来的结果可以把k保持住。
(6)这个网格是二维平面网格(宽度只有一层),对于Yang2009的方法,能否直接用于二维网格还没有验证,并且目前对比的结果都是取计算域中间的结果,不考虑边界的影响。
@疏影横斜水清浅 在 中性大气环境湍流动能的自保持 | 附有算例下载 中说:
@李东岳 测试的网格如下,网格尺寸比较大
convertToMeters 1; vertices ( (0 0 0)//0 (5000 0 0)//1 (5000 500 0)//2 (0 500 0)//3 (0 0 1)//4 (5000 0 1)//5 (5000 500 1)//6 (0 500 1)//7 ); blocks ( hex (0 1 2 3 4 5 6 7) (500 50 1) simpleGrading (1 10 1) ); edges ( ); boundary ( inlet { type patch; faces ( (3 0 4 7) ); } outlet { type patch; faces ( (1 2 6 5) ); } topWall { type patch; faces ( (2 3 7 6) ); } flatWall1 { type wall; faces ( (0 1 5 4) ); } front { type empty; faces ( (4 5 6 7) ); } back { type empty; faces ( (3 2 1 0) ); } ); mergePatchPairs ( );
还是有挺多疑问,请各位大佬解惑
-
@小李的幸福生活 由于我主要不是研究这个内容,后面没再尝试了。我的理解是全尺寸和缩尺转换,相关的参数应该都要转换。一个简单方法验证变换的对不对,可以把缩尺后的
k剖面画出来,看下数量级是否合理的。比如现在算全尺寸,平均风速取$U_{avg}=40\ m/s$,湍流强度取$I_u=10\%$,近似取三个方向湍流强度一样大,那么估计的湍动能数量级应该为:$k=\frac{3}{2} \sigma_u^2=\frac{3}{2} (U_{avg}I_u)^2=24\ m^2/s^2$。比如7#楼中HW07方法用的目标值,感觉有点偏小,主要原因全尺寸的平均速度剖面取值也偏小只到12m/s这个方法简称HW07,参考的是
D.M. Hargreaves and N.G. Wright 2007,目前这一套方法计算出来的结果可以把k保持住。