如果用DPMFoam求解稀相流会怎么样？误差大么
-
@dzw05 在 如果用DPMFoam求解稀相流会怎么样？误差大么 中说：
粒子运动方程中根本没有出现连续相的压力
这个是问题的根源。因为存在俩套方程：
-
第一种是你说的，不存在连续相的压力，DEM可以这样模化：
\begin{equation}
m_\mathrm{dpm}\frac{\partial \mathbf{U} _ \mathrm{dpm}}{\partial t}=\mathbf{F}_ \mathrm{drag}+\frac{\mathbf{g}(\rho_\mathrm{dpm}-\rho_\mathrm{c})}{\rho_\mathrm{c}}+\mathrm{Others}
\label{gra}
\end{equation}在这个方程中，如果不考虑F，那么就可以模化重力和浮力的效果。这就是DPMFoam中采用的方法。
-
另一套方程是
\begin{equation}
m_\mathrm{dpm}\frac{\partial \mathbf{U}_ \mathrm{dpm}}{\partial t}=\mathbf{F}_ \mathrm{drag}+m_\mathrm{dpm}\mathbf{g}+\frac{m_\mathrm{dpm}}{\rho_\mathrm{dpm}}\nabla p_\mathrm{c}+\mathrm{Others}
\end{equation}如果采用这一套方程，其中的压力需要为静水压力。
目前我在研究第二种方法。Fluent以及OpenFOAM中选用的第一种方法。参考Fluent理论指南。
-
-
@dzw05 参照 多相流数学模型 http://dyfluid.com/docs/multiphase.html 3.3 连续相模型之欧拉模型（宏观模型）：
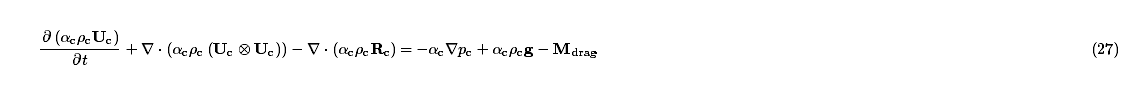
“从可压缩动量方程出发，假设密度是常数，那可以将密度提出来，就是现在采用的不可压缩动量方程形式啊，为什么会默认密度为1呢？”
假设密度是常数，那么即使将密度提出来，DPMFoam求解器中的动量方程中压力项还少除以了一个密度（除非密度是1）“具体来说在Openfoam中，particleForces中的pressureGradient这项才是浮力项。”
颗粒所受的浮力在颗粒所受重力项中已经体现（）：
pressureGradient就是单纯的压力梯度力，但是大小和浮力相反（可参考颗粒在流体中的受力分析 https://wenku.baidu.com/view/171125dcd15abe23482f4d93.html、董长银-牛顿流体中的固体颗粒运动模型分析及应用https://wenku.baidu.com/view/8fafedfef705cc175527097a.html）“DPMFoam动量方程中的重力项有一部分是流体的重力，另一部分和pressureGradient这一项组合起来作为浮力。” 您是说连续相的动量方程中的重力项要被拆分吗？据我调查，颗粒所受重力中已经考虑了流体的浮力影响，那么，颗粒对流体应该有相反的作用力（体积力的源项），那么连续相动量方程里的重力项似乎可以解释了，是作为颗粒的耦合项加入的。
@东岳 “pressureGradient是粒子上下表面引致的压力差项，粒子若非常小，则可忽略。但若重力gravity若被忽略，则完全没有浮力影响。” 颗粒浮力的影响通过连续相的密度以及重力加速度体现出来，关于https://wenku.baidu.com/view/8fafedfef705cc175527097a.html文献中提到的考虑了压力梯度力后，浮力项不起作用了，因为两者大小相等，方向相反，在openfoam中还没有验证，应该根据具体案例和压力分布相关
-
@dzw05
“没错，在离散相的gravity中，表达式是massg_(1.0 - p.rhoc()/p.rho())，即考虑了连续相和离散相的密度比，这个是浮力的%(#c43d3d)[主要来源]。” 浮力还有哪些其它来源呢？
“如果单纯的将连续相动量方程中的重力g删除，而不是设为0，那么其实并没有影响粒子浮力的计算，因为粒子运动方程中根本没有出现连续相的压力。” 粒子运动方程中出现的连续相的压力，不是可以通过压力梯度力来体现出来了吗？这样一来，连续相动量方程中的耦合项或者压力项需做相应调整了。@东岳 您提出存在下面的两套方程，是等效的吗？
-
这俩套方程都是文献中看到的，可以参考本帖24楼。我自己的求解器中采用这种形式
\begin{equation}
m_\mathrm{dpm}\frac{\partial \mathbf{U}_ \mathrm{dpm}}{\partial t}=\mathbf{F}_ \mathrm{drag}+m_\mathrm{dpm}\mathbf{g}+\frac{m_\mathrm{dpm}}{\rho_\mathrm{dpm}}\nabla p_\mathrm{c}+\mathrm{Others}
\end{equation}俩种形式可以互相转换。依据$p=p_0+\rho_\rc \bfg\bfh$即可相互推导
-
\begin{equation}
\label{DPM} m_\dpm\frac{\rd \bfU_\dpm}{\rd t}=-\frac{m_\dpm}{\rho_\dpm}\nabla p+m_\dpm\bfg+\frac{m_\dpm}{\rho_\dpm}\frac{3}{4}\frac{C_\rD\rho_\rc}{d_\rd}\left|\bfU_\rc-\bfU_\dpm\right|\left(\bfU_\rc-\bfU_\dpm\right)+\mathrm{OtherForces}.
\end{equation}
伯努利：
\begin{equation}
\label{bnl} \nabla p=\rho_\rc\bfg
\end{equation}
代入：
\begin{equation}
\label{DPM3} m_\dpm\frac{\rd \bfU_\dpm}{\rd t}=m_\dpm\bfg\left(1-\frac{\rho_\rc}{\rho_\dpm}\right)+\frac{m_\dpm}{\rho_\dpm}\frac{3}{4}\frac{C_\rD\rho_\rc}{d_\rd}\left|\bfU_\rc-\bfU_\dpm\right|\left(\bfU_\rc-\bfU_\dpm\right)+\mathrm{OtherForces}.
\end{equation}
-
-
-
