Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam

wwzhao

@yhdthu 可以做fieldAverage，然后用生成的pMean来计算Cp。

yhdthu

@wwzhao 是的，我就是这么做的

yhdthu

还有个问题，请问LES网格大小是怎么确定的呢？我是根据kolmogorov理论确定的delta，即：

L0/6 < delta < 60L0Re^(-3/4)

(L0是积分尺度)

还有壁面附近是怎么处理的呢？

依据此做的网格，感觉网格有点粗，不知你是怎么确定的呢？

random_ran

@yhdthu

近壁的地方是最难处理的，因为在这些地方没有大涡。LES也可以用wall function来避免太多的计算量，但是wall-resolved的LES的网格和DNS非常接近。

通常对壁面网格的控制是用无量纲墙距离 (yplus/y+)来标定。这个量的确定和雷诺数密切相关。对于wall-resolved的LES，y+<1是文献中最常提到的。对于用wall function的例子，y+可以放到30到200之间用来避免buffer layer，不同的wall function 还是有一些不同的要求。

对于stream-wise, span-wise，wall-resolved 的LES还有更高的要求。Georgiadis (2010）给出的建议是:

50< Δx+<150; Δy+<1; 15< Δz+<40

POINTWISE, NASA都给出了依据y+计算第一层网格高度的公式。

可以看看这个帖子。

yhdthu

对于方形计算域，我猜是不是因为网格过渡均匀性做的不好导致的Cd偏大？

Junhua PAN

方形计算区，o型网格覆盖3D~4D范围，再加上尾迹区加密，结果应该是一样的。主要原因，猜测是非正交网格对涡解析不够，造成Cd或Cl差异。至于涡对Cd和Cl影响，可以参考吴介之老师的涡动力学。

random_ran

当时的计算结果高了大概10%~20%，当时试了很多：
 Fixed grid jump transition area
 Use LUST scheme for the convective terms
 Implement LES turbulent models such as TKE and Smagorinsky model
 Use nutLowReWallFunction instead of nutUSpaldingWallFunction
 Increase computational domain
 K and nut parameters
 Boundary conditions: two cyclic with two slip wall conditions

最后的结果发现换网格的效果是最好的。圆形计算域的正交性更好一些。而且这个计算域用自动生成都可以做到很好的质量，何乐而不为呢？

yuan_neu

@Junhua-PAN 求书名，网上没搜到

yuan_neu

@random_ran 想请教一个问题，如果用symmetry网格的话，对计算结果影响大吗？

random_ran

如果单纯从均值Cd的大小上看，这两个边界条件，对于我所用的那个网格并没有太大影响。

我最开始的时候也是用过symmetry的边界条件，但是我觉得slip-wall 的边界条件可能更适合描述我当初对这个问题的理解。

后来我发现这个研究方向上的文献中，绝大多数人在span-wise都是用cyclic的边界条件。用cyclic边界的条件的优势之一就是能把模拟的有限长度的圆柱，当成无限长来出来。换句话说就是end-effect上有很强的优势。这个即便是做风洞实验都无法克服的问题，因为风洞中都要用end-plate来矫正端部对流场的影响。

Yeo, DongHun, and Nicholas P. Jones. “Investigation on 3-D Characteristics of Flow around a Yawed and Inclined Circular Cylinder.” Journal of Wind Engineering and Industrial Aerodynamics 96.10–11 (2008): 1947–1960. Web.

这篇文章中3.1节讨论了 slip-wall 和 cyclic wall 对涡结构的影响。作者发现在cyclic边界条件受边界的影响要小，因此cyclic边界条件能更好模拟三维圆柱绕流这一经典问题。

yuan_neu

@random_ran :kiss: :kiss:

Junhua PAN

@yuan_neu Vortical Flows 第9章

程迪

@random_ran 在 Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam 中说：

时的计算结果高了大概10%~20%，当时试了很多：
 Fixed grid jump transition area
 Use LUST scheme for the convective terms
 Implement LES turbulent models such as TKE and Smagorinsky model
 Use nutLowReWallFunction instead of nutUSpaldingWallFunction
 Increase computational domain
 K and nut parameters
 Boundary conditions: two cyclic with two slip wall conditions
最后的结果发现换网格的效果是最好的。圆形计算域的正交性更好一些。而且这个计算域用自动生成都可以做到很好的质量，何

你对比的是啥文献，用的什么边界条件呀？

我看有个早期文献是用FVM加变换算的无穷大边界的，和一般的有限大小边界还不一样。

如果你考虑正交性，你在fvScheme中加修正了么？梯度用的啥？OF对非正交和skew都有相应的修正方法，可以提高一点儿精度。我写过一个小帖子OF修正小结，你可以尝试搞搞边界条件类型和fvScheme中的修正。

random_ran

主要参考的是
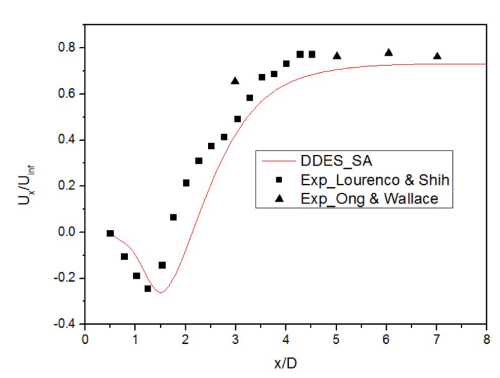
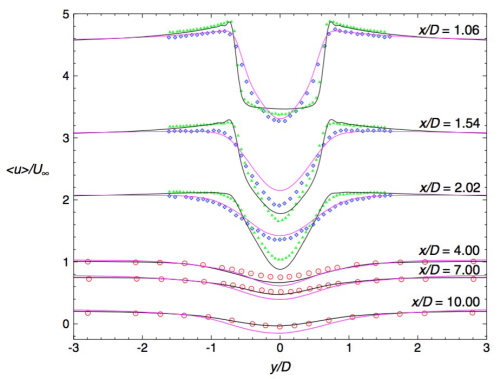
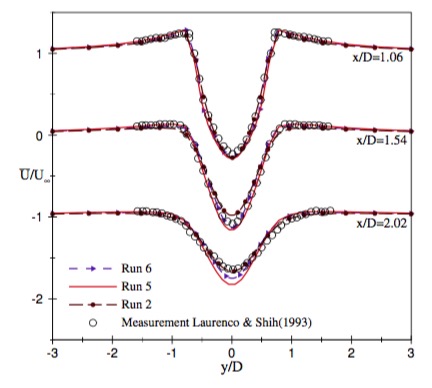
Lysenko, Dmitry A., Ivar S. Ertesvåg, and Kjell Erik Rian. “Large-Eddy Simulation of the Flow over a Circular Cylinder at Reynolds Number 3900 Using the Openfoam Toolbox.” Flow, Turbulence and Combustion 89.4 (2012): 491–518. Web.

Lysenko (2012) 用的是：

inlet: 层流
outlet: wave-transmissive conditions （不太明白，我用的是 pressure:fixValue=0）
span-wise: periodicity
cylinder: no-slip

能提供一下那篇早期文献吗？

当时没有考虑正交性问题, 关于梯度的离散是这样设置的:

gradSchemes
{
    default         Gauss linear;
    grad(nuTilda)   cellLimited Gauss linear 1;
    grad(U)         cellLimited Gauss linear 1;
}

这个贴子当时是在算Re3900的时候遇到Cd的过高估计，最终发现换一套网格和用dynamic kEquation 就能把Cd预测的很准了，所以那段研究就没有再进行下去了。

有时间我会再把以前的那套网格用你提供的方案再算算，看看结果会怎么样。

程迪

@random_ran
waveTransmissive类似特征边界条件，反正Wikki是这么说的。可能更加有物理意义吧。

yhdthu

你好，我用DDES-SA模型做出来的模拟图如下：

这个对的不是很好，另外流向平均速度就更离谱了，选取了流向三个位置，
x / D = 1.06;x / D = 1.54; x / D = 2.02，如下

我对比了两个文献，其中一篇是你推荐的，如下：

我不明白，都是无量纲分布，怎么差别这么大？我的计算问题会出在哪呢？谢谢

程迪

@yhdthu

模型与模型之间可能是不一样的，参考NASA TMR 关于SA模型的实现，https://turbmodels.larc.nasa.gov/spalart.html#sa，SA模型有10种左右变种。

OF实现的是SA-fv3.

yhdthu

@程迪你好，我用的模型是DES类模型，在我取点处已经切换成LES模型计算了，另外无量纲分布怎么会随着模型变化呢？把它变成有量纲形式就可以看出来不可能，分布是一定的，可以参考实验

yhdthu

@yhdthu 经过查阅文献，确认了文献纵坐标是废的。。

random_ran

@yhdthu

我觉得你第一个图做得已经很棒了！比对的是两组实验数据，你可以再加上数值模拟方面的数据就更好了。

如果你想再提高精度，更精密的网格肯定逃不了。另外湍流的模型的选择对结果的影响很大。还有就对流项的离散选择。关键是看你模拟的目的是什么。

Ps: 文献纵座标是废的是什么情况？能详细说说吗？
Ps2: 网格数量是多少？求解核心数？计算时间？边界条件如何？不知能否分享一下你的经验？

CFD中文网

Cd计算不准的问题-LES-Re3900-三维圆柱绕流-pisoFoam