LES和RANS中,离散的对象是相同的吗?
-
显然不一样。
RANS的平均实际上是系综平均,ensemble average,这类似于一种概率上的平均。比如在某一点某一时刻上的one-point one-time速度的PDF,对于不同的速度值(三个方向上)进行积分操作,平均得到的是期望值。
所以我们实际上是有种东西叫Unsteady RANS。对于统计学静态问题,我们还可以进行时间平均操作,从而完全去掉unsteady term。
对于各向同性的湍流,实际上还有一种Volume average的东西。
对于LES,它不是进行平均操作,不是进行平均操作,不是进行平均操作。
回到Kolmogrov的模型,见下图
横轴是波数,纵轴是能量的对数。我们看到的是,湍流动能的主要存在惯性区间之前,耗散区间所存储的湍流动能是很少的。对于DNS,网格的解析尺度是需要小于Kolmogrov尺度的,然而对于实际的问题,这么细小的网格是不现实的。那么人们会退一步想,我不考虑所有的尺度,我只考虑到耗散区间之前一点点,仅仅考虑energy containing的区间不就可以得到将将够的数值解么?注意到纵轴是对数,所以耗散区间,也就是小尺度的涡所包含的能量是非常少的。这是我们称这种方法叫做大涡模拟的原因。对于LES,我们进行的操作叫做filtering,这个操作,从数学上将小尺度的涡给过滤掉,然而它本质上还是一种比较直接的湍流的模拟。对应RANS中的平均速度值,我们这里成为filtered速度。注意到,这里fileted速度是一种即时值,意味着,如果我们需要再次进行平均才能得到统计信息。
对于多数人,对于RANS和LES的误解来源于,它们的方程形式是极其相似的。如果仅仅从方程的形式,LES的Smagotinky模型仅仅相当于RANS中最简单的代数模型,那么LES又是如何能够取得比RANS更高的精度呢?
回到你的问题,离散的时候离散的对象当然不一样,即时形式一样(使用RANS的代数模型和LES的Smagorinsky模型),它们也是本质上完全不同的东西。更何况,RANS当中还有各种各样的k-e,k-w,e-w之类的东西,LES也有着Dynamic Model,one-equation model之类的东西。
-
@浪迹天大 新的理解:LES 和 RANS 的本质区别就是LES的粘度比后者小,并且还会随着网格的减小进一步减小。而粘度,就相当于把扩散项的作用加强的程度。LES 的粘度小,所以扩散作用弱,流场越活跃,故能捕捉到更多的涡。我感觉这大概就是 Boussinesq 假设的缺陷吧。所以有人提出不基于 eddy-viscosity 的湍流模型。我只了解LES,这里举个non eddy-viscosity 的 SGS 模型的例子:dynamic structure 模型
$$\tau_{ij}=C_{ij}k_{sgs}$$
$$k_{sgs}=\frac{1}{2}(\bar{u_iu_i}-\bar{u_i}\bar{u_i})$$
$$C_{ij}=2\frac{G_{ij}}{G_{kk}}$$
$$G_{ij}=\frac{\partial \bar{u_i}}{\partial x_k}\frac{\partial \bar{u_j}}{\partial x_k}$$这里的 dynamic structure 模型就与一般 SGS 模型不同。
不知道我的理解对不对。希望一起交流:happy: -
@ywj123450 在 LES和RANS中,离散的对象是相同的吗? 中说:
LES的粘度是和网格相关的,网格越小,粘度越小。但是我还是没理解,为什么粘度小就更准确。贴上李新亮老师的CFD课程:http://pan.baidu.com/s/1qYrJh0o
你看这个图:
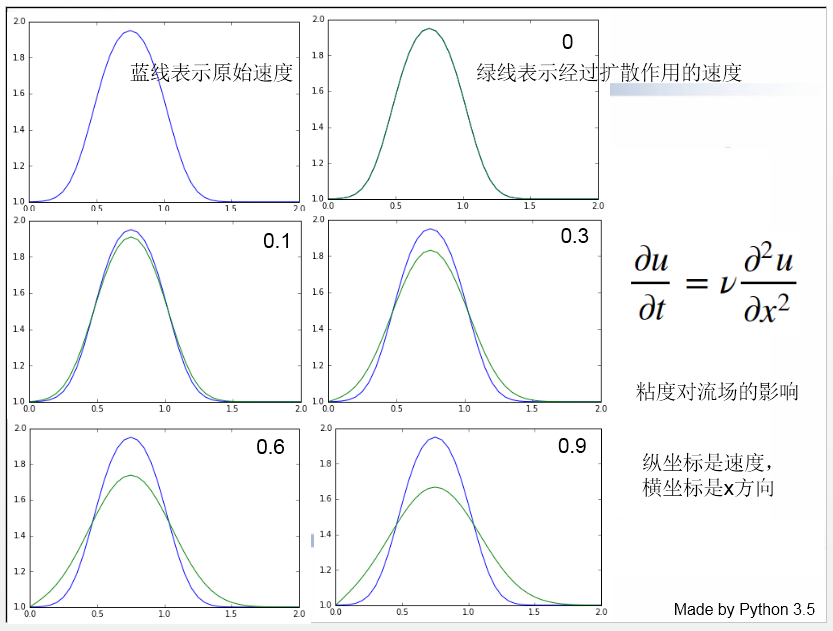
扩散项的作用就是让流场变得更均匀。
粘度大的话,那些细小的流场结构就被抹平了啊。 -
\begin{equation}
\frac{\partial \mathbf{\bar{U}}}{\partial t}+\nabla \cdot (\mathbf{\bar{U}} \mathbf{\bar{U}})=-\nabla \frac{\bar{p}}{\rho}+\nabla \cdot(\nu \nabla \mathbf{\bar{U}}) + \nabla \cdot \left( \rho\left( C_{\mathrm{SGS}} \Delta \right)^2 \sqrt{2\bar{S_{ij}} \bar{S_{ij}}} \bar{S_{ij}} \right)
\end{equation}从最终方程来看,LES和RANS确实就是湍流应力的不同。虽然RNAS用的是时均,LES用的是滤波。但是最终表现只在湍流应力项。再通过将速度和湍流应力联系起来的时候,附加了大涡粘度。RANS和LES都存在大涡粘度,并且都需要模化。在LES中,大涡粘度和网格大小以及形变率有关。
从物理来看,LES和RANS的区别并不是粘度不同导致的。LES源自对NS方程进行滤波。RANS源自时均。在LES方程推导最开始最开始的时候,就引入了截止尺度。因此LES封闭的时候和网格是高度相关的。RANS封闭的过程中不需要截止尺度,因此和LES,DNS不同。RANS并不是网格依赖模型。
这里有几个图是LES和RANS模拟的,可以看出流场是非常不同的。明显RANS是经过时均的流场。也正如@showhand 提及的:
对于多数人,对于RANS和LES的误解来源于,它们的方程形式是极其相似的。如果仅仅从方程的形式,LES的Smagotinky模型仅仅相当于RANS中最简单的代数模型,那么LES又是如何能够取得比RANS更高的精度呢?回到你的问题,离散的时候离散的对象当然不一样,即使形式一样(使用RANS的代数模型和LES的Smagorinsky模型),它们也是本质上完全不同的东西。
所以通过降低粘度,RANS的结果会和LES相同这种说法非常具有挑战性。另外,湍流粘度应该是计算出来的(比如从k和e计算,或者LES中从劫持尺度等系数计算),计算中如何认为的降低粘度?
用的 RANS, 说把粘度调小了,就能获得与 LES 类似的效果
很有意思,which paper?
-
这篇文章主要强调的是 RANS turbulence model does not always yield an ensemble average result,而一般认为 RANS 模型得到的是系综平均后的结果,是“稳态”的。比如那个二维圆柱绕流的例子,他用的是标准 k-epsilon 模型,一般认为标准 k-epsilon 无法得到涡街(前一阵子群里的 Him 也曾这么说过),不过他这里通过加密网格,使用中心差分,模拟出了涡街。但是,这里有很多细节没有提及,比如边界是怎么处理的,y+ 是多少等。标准k-epsilon模型,应该是要求 y+ 在对数区的,如果他加密得过分了,y+ 到了层流底层,然后还采用了一些类似 enhanced wall treatment 这样的方法来处理边界(其实主要就是计算边界附近的湍流粘度),那他这个还能不能算是标准 k-epsilon 模型就要打问号了。
